主题:“魔改”《白蛇传》 -- 给我打钱87405
你是个天才,写的东西哦,多数我看不下去了。脑子确实不行。不费力气了。
只是提醒你一下,关于你那个圆和正方形的周长,从而论证微积分原则的错误。
数学分析的基础是极限求值。有些极限可以求,有些不可以。可求值的是收敛的。你那个圆外正方形的周长就是一个收敛的级数极限,它的收敛值是圆的周长,而不是你的直观看法。
这个级数的具体表达和极限算法,你可以请教北纬同学。他是数学专业的。
@北纬42度
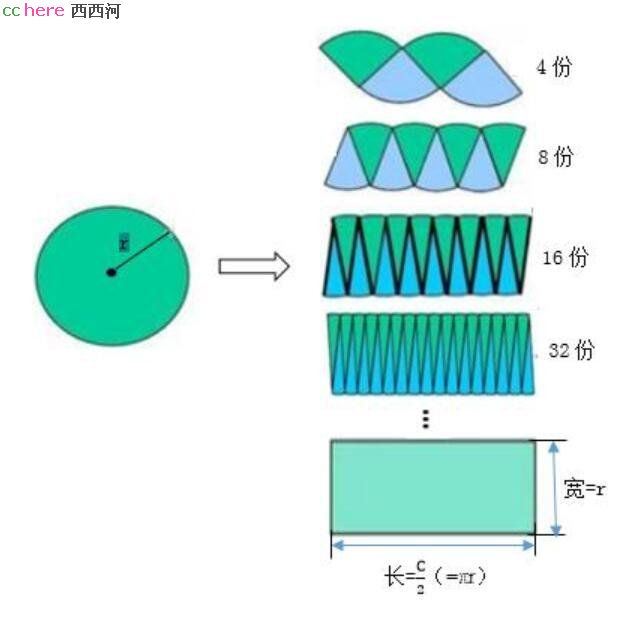
这张图我相信大家都是有印象的。嗯,但你就在这【学错了】。你的老师告诉你,这样这样就推出了圆的公式,π*r*r,你老师错完了。
圆的面积公式,只要你明白什么叫缩放,你自己就可以建立,圆的面积公式一定是k*r*r。这就跟我之前讲的牛顿第二定律一样,F=ma这个公式你自己也有能力建立,因为一个不变的力一定对应一个不变的运动,可能你不知道这个不变的运动中的不变具体是什么,但会有一个最基础的公式F=k*X,k是系数,X就是就不变运动中的那个不变。
圆的面积公式在某种角度来看,比长方形还要容易,因为圆这一规则图形只能缩放,而影响因子只有一个就是半径。我相信有许多人压根就没有学会这项最基础的知识。长方形的面积公式S=a*b它所描述的是如果b不变a变大一倍那么S就变大一倍,如果a不变b变大一倍那么S也变大一倍,如果a和b同时变大一倍那么面积就变成了之前的4倍(这种情况属于缩放)。这个你明白,对不对?你搞错的地方是你认为这是高智商的数学家发明出来的,对不对?
我相信你读小学的时候老师就让你做过比较,一张纸片是3cm*6cm,另一张是4cm*5cm,比比看,哪张更大。你不知道的是,你的老师从一开始就在误导你。因此,你学到后面你仍然没有发现,长方形面积公式S=a*b首先是对这一长方形的描述。现在看看,难道不是这样吗?
他应该一上来就给你讲缩放。缩放是动作,一个图形经过缩放之后变成另一个图形,这两个图形在数学就叫相似。如果你的老师一上来就给你讲缩放,你是不是自己就知道边长放大一倍,【那个】就放大了4倍?【那个】就是面积嘛,给你一个词汇就行了嘛。
给你讲完缩放之后再给你讲其中一条边变成1倍,问你面积会变成多少?也是1倍,对不对?老师再给你一引导,你就意识到了,你总在回答倍数,对不对?
在这样的基础上给你一引导,你是不是就明白了S=a*b描述的是长方形边长和面积的数量关系?再给你引导一下,你是不是就能猜出来所有的面积公式都是这个套路?
等你学完了这个,老师问你:圆的面积公式长啥样呢?你是不是自己就能回答出来是k*r*r?当然你会把系数k漏了,这不要紧的,老师会让你明白的,因为三角形面积公式也有系数1/2。
等你自己能回答出来圆的面积公式k*r*r,你再看这张图的时候你想到的是什么呢?
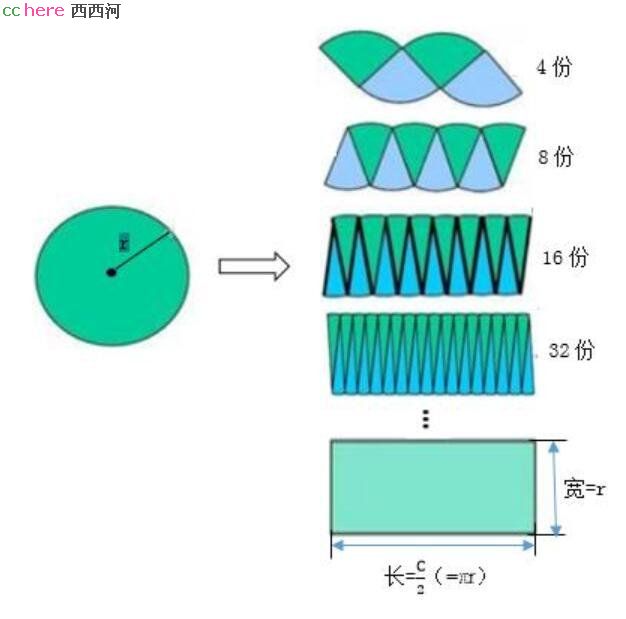
这并非是在求圆的面积,而是在建立圆的周长和面积之间的联系,换言之,是在说k1=k2=π。
你从一开始就学错了,所以你会产生错觉,认为没点数学细胞是学不会的。
现在,你猜一下,你的老师的老师的老师,为什么没有像我那样给你传授数学的基础知识,反而把上图包装成【求圆的面积】?
不妨再讲一个例子。
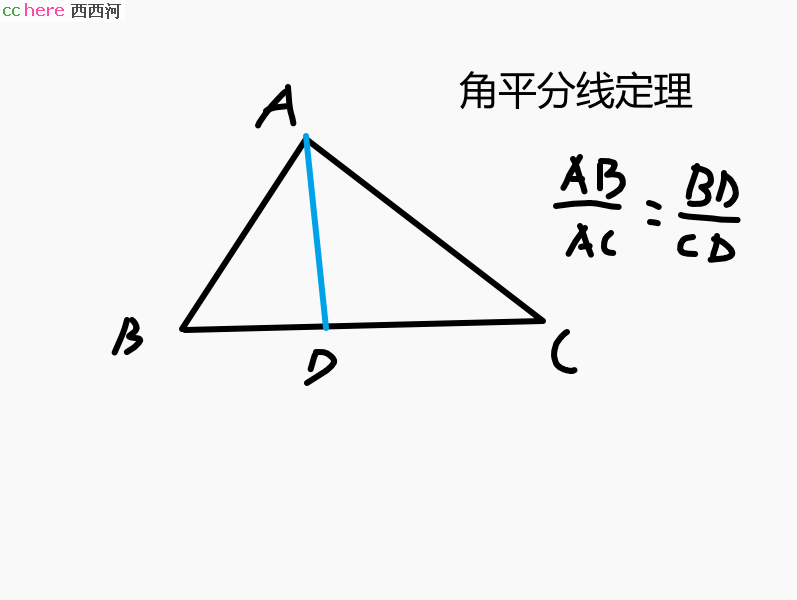
AD平分角A,于是有AB:AC=BD:CD,这就是角平分线定理。
好,老师告诉你这个定理,你就会问:凭啥呢?老师就说我给证明给你看。
但是,如果你明白一个基本的道理:任何一个结论当中一定含有提示,你自己就可以完成逻辑推理。你把AB:AC=BD:CD一看,噫?这个BD:CD不就是两个小三角形的面积比吗?等高不等底嘛。这样来说,AB:AC也是两个小三角形的面积比啊。嗯,让我再看看。你的脖子一扭,发现了,换个角度,这两个小角形是同底(AD)不同高,高之比就是AB:AC。任务完成。
但是,你的老师却给你秀了一番,他是这样证明的:
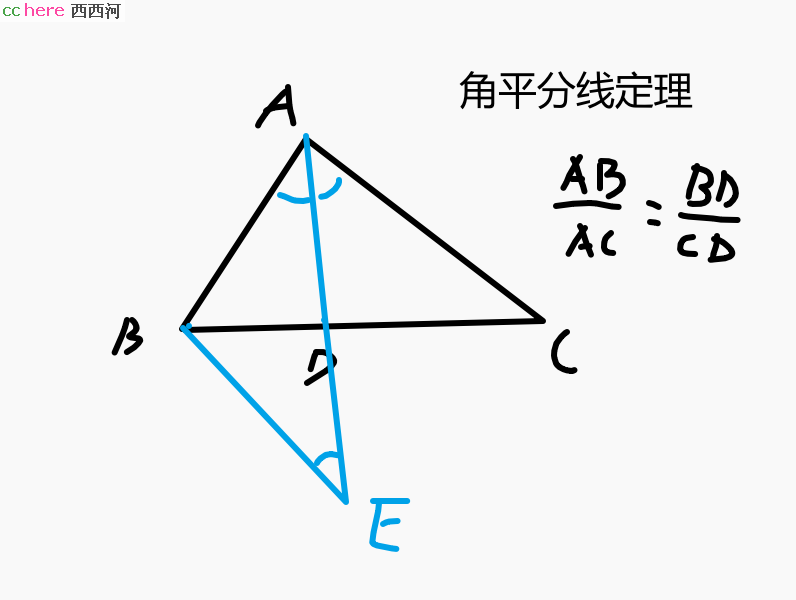
延长AD至点E,BE平行AC,所以三个角相等(平行),所以AB=BE(等腰三角形),所以BE:AC=BD:DC(相似三角形),所以AB:AC=BD:CD,证毕。
秀完之后问你牛逼不牛逼,你大呼牛逼。
其实这第二种证法(还有更多)只是在玩,为了证明而证明,是根据结论解构出一条逻辑路径。玩,本身是可以的,也是需要的,但玩是玩,然而你老师却将其吹成神技。
知道你老师为什么要这么做吗?因为他要证明你是个傻逼,即你身上没有数学细胞。
我总结了一下,西方人是如何通过教育来杀害我们的,三大项:
1.把关键的知识点改一下,比如k1=k2=π;
2.在方法上误导你,把正招说成一般般,把雕虫小技吹成神功;
3.从精神上摧毁你,你不是学XXX的料,你没有相关的细胞。具体手法就是抽梯子,让你从平地直接跳上房顶。你自然跳不上去,这样他就证明了你是个天生的蠢货。
当然,你的老师也是受害者,他只是在完成西方人给他安排好的任务,继续残害下一代。
另外,关于“k1是否等于k2”这个问题再多讲几句。
那篇帖子你已经看了,里面有个证明是sinθ<θ。他的证明是:因为弧长大于弦长,所以弧长大于弦长。当然,如果他直接这么说,你当场就笑瘫了,于是他改了一下,因为弧长大于弦长,所以sinθ<θ。
西方人说k1=k2=π用的是一模一样的手法。他先用微积分推导出k1=k2=π,你说你不信,他说好办,我用微积分证明给你看,一定是k1=k2=π。只不过这个圈子绕得大,圆的面积公式你是小学的,微积分是大学学的,中间你的所谓学习就是在绕圈。为啥小学四年级就能学完微积分课程呢?因为人家没有绕圈。不过,微积分学没学的也没有什么,这是因为N多微积分公式都是建立在k1=k2=π之上的,可如果不是这样呢?如果不是这样,那么多微积分公式就全是屁。
我的重点在讲,西方人是来要咱们的命的,许多人坚信的客观的自然学科知识,数学、物理、化学、生物、地理,其实还包括经济学——经济学被他们包装成了自然学科,门门都有剧毒。
“换个角度,这两个小角形是同底(AD)不同高,高之比就是AB:AC。任务完成”
为什么高之比就是AB:AC?AB和AC又不是高,高需要垂直于AD。你需要证明两个高的比和AB,AC的比值相同。
小学生做题都知道:题里给的条件没有用,基本做出来的就是错的。你看你用了AD是等分角这个条件了。你那个推倒, 岂不是任意给一个AD这个结论都对?
这么写考试只能是零分。
不断细分下去“对角线”就成了8:
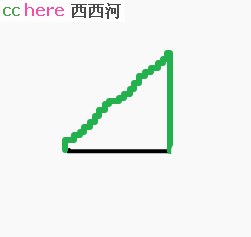
然而,这个“对角线”是假的,是【看起来像】。前文我已经明确指出:欲从A点走到B点,不论你选择哪条路径,只要你是【左右交替变向】,总步数总是8步。即,我明确指出这是折线。
再来看这张图:
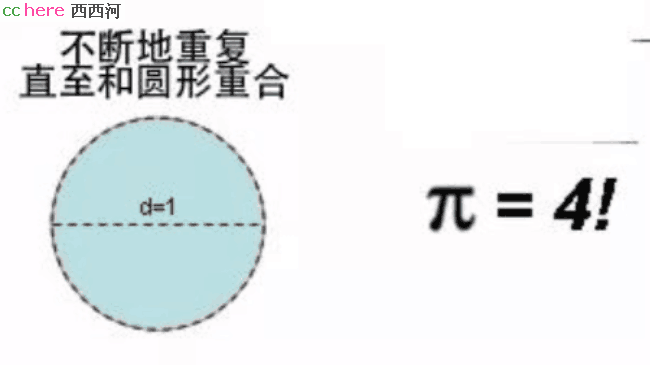
如果我把内接圆去掉,你看到的是什么呢?
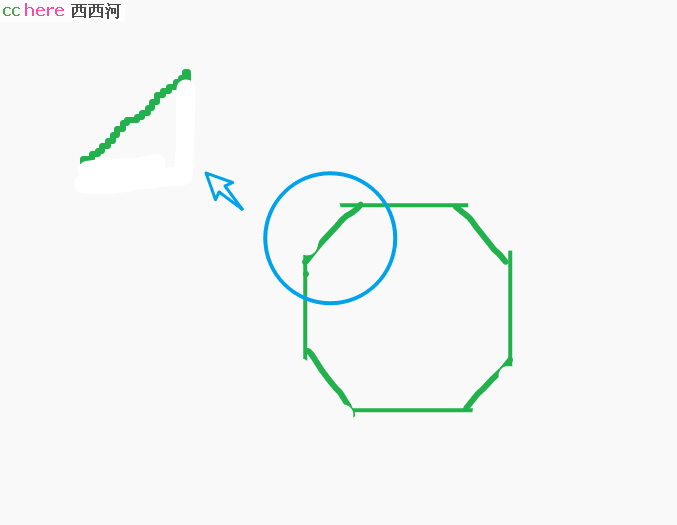
我把内接圆又重新画上,你看到的是什么呢?
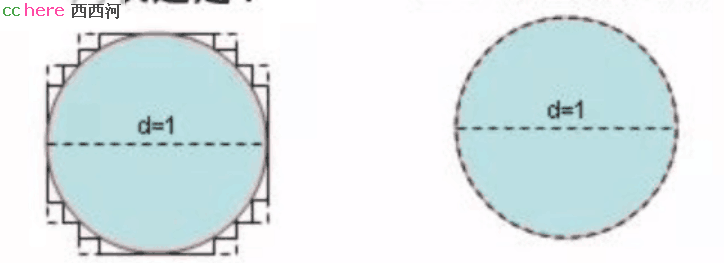
小结:
一种情况,可以把折线诱导成直线也就是“对角线”,另一种情况,又可以把同样的折线诱导成曲线也就是“圆”。
so,微积分是怎么回事?
本帖一共被 1 帖 引用 (帖内工具实现)
详情可以看这里:https://zhuanlan.zhihu.com/p/116428479
核心在这里:
那么,这个证明的漏洞在哪里呢?其实方形的边无论切分成多少个阶梯,都不可能和圆弧完全重合,而这些直角的边其实都能还原为之前的方形。
这里面就涉及到微积分的问题:无穷小值,我们知道1/n,当n趋向于无穷大时,其值是0,然而此处有n个无穷小(1/n),其值是不为0的。同时也说明了:误差是不可以累积的
真正想了解这个问题的答案,可以看这本书:

顺便说一下,按照我的理解,编号老兄提到的微积分的问题要等到柯西在19世纪的三篇论文才得到初步解决

之后,魏尔斯特拉斯,戴德金与康托尔都有对柯西的论文继续完善。
PS:这里问题,按照我的理解,涉及数学的本质,如果编号老兄不是数学专业,能够独立思考而提出这样的问题,确实厉害!
一个鸡腿太划算了,一个烧鹅腿加一瓶二锅头都可以啊!😄😄😄
一支鸡腿,先挂账上。
嗯,你得有点耐心,因为会有一些重复的内容,但我这次给整合到一起了,从骗术说起。

上面这张图还记得吧?如果把格子再画小一点,“对角线”是不是就成了8?也就是“对角线”等于两边之和。
但如果我【直接】即第一时间给你看下面这张图,你的看法是怎样的呢?
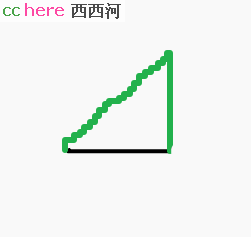
你会说,这怎么可能呢?对角线在此处的名字叫斜边,斜边是不可能等于两直边之和的,这是你坚不可摧的认知。
因此,我怎么来完成欺骗呢?我会这么干。
先给你看第一张图,这样你就接受了8步的结论。接下来一步是我能完成欺骗的关键一步,我会开始说省略语,我会把“欲从A点走到B点,不论你选择哪条路径,只要你是左右交替变向,总步数总是8步,对吧?”【省略成】“不管怎么走,总是8步”。我还有一个配合的动作,那就是慢慢来,格子是一点一点的变小,起初是细分成是4个,然后细分成9个,然后细分成16个,每次我都重复“不管怎么走,总是8步”。最后,我给你上下图:

你就会“哇,对角线是8!天呐,这是怎么回事?”你(至少)混乱了。你为什么会混乱呢?因为有三样内容搅和在一起:
1.不管怎么走都是8步
2.对角线一定大于两边之和
3.你的视觉让你觉得那是直线
1跟2是相斥的,这里面哪个才是对的,就看你用的是脑子还是眼睛,但我会不断的引诱你去看,引诱你扔掉大脑只用眼睛。
现在来看所谓的“求圆的面积公式”,如下图:
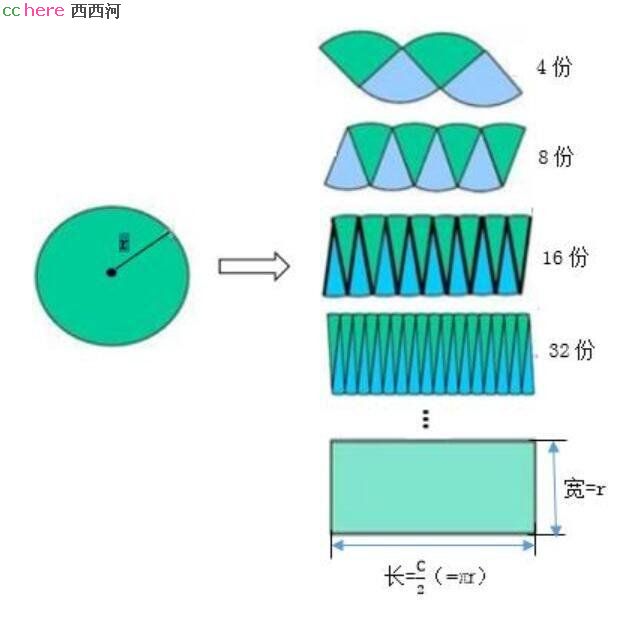
你是用眼睛接受的还是大脑?用眼睛。
上面这一整套都叫软,我必须另有一手硬:“想不想考高分?想不想毕业?”软硬兼施,你就被我拿下了。
现在的你想想看,那个“求圆的面积公式”的欺骗手法是很糙的,直接从曲跳到直,并不是曲线——折线——直线,为什么呢?因为他是来骗小学生的啊。等你进了大学就不一样了,他要上花点样才行,比如开始给你讲深邃,微积分思想是很深邃的一般人理解不了的,这意思就是说你背下来就好了反正你也理解不了,这句话其实在说“你是个残废,你只能靠别人喂饭给你吃”,但他说得很“客气”你听不出来然而你会照做,因为他还有一招,“想不想毕业?”这前面已经说过了。
当然,仅仅是给你讲“微积分思想是很深邃的一般人理解不了的”还不够,还得鱼目混珠才行。
拿出1/2+1/4+1/8+……这个式子,问你一名初学者,你十有八九会说“这加不完啊”。他知道你会这么认为的,于是他微微一笑:1/2+1/4+1/8+……=1,你要不信,我证明给你看。
他为什么不告诉你“一根棍子每次截一半可以一直截下去”呢?因为他要向你推销他的【证明术】。这是其一。其二,他开始给你植入“不断细分”(换成高大上的词就是求极限)这一概念,将来,你就会把“不断细分”这一概念迁移到微积分上面去,你就会接受微积分。
“不断细分”确实是真实存在的,然而有一种是真的,比如“一根棍子每次截一半可以一直截下去”,还有一种是假的,比如化直为曲。为了进一步欺骗你,他会说“这个求极限啊,它是有使用范围的,有的极限数列收敛,有的发散”,白手套已经准备好了。可是,他为什么没有去回答“k1=k2=π”这是收敛数列还是发散数列呢?
我这么骗你,至少可以把你搞晕。就算你后来明白了你上了大当,你也已经老了,你的时间全消耗在迷宫当中了。你老了,你把你上过的当说给别人听,会有几个人相信你呢?
现在,我再说一次:骗死你太容易了,现在相信了吧?N多人自视过高,服不服?N多人自认为的谦虚谨慎实质上是假的,服不服?
你不研究人家是怎么欺骗你的,你就总认为你不会上当的,你上了一次当你不会上第二次当。
骗术就讲到这里,下面讲点正经的。
直线,只存在于我们的意识当中,圆弧也一样。所以,什么叫直线,什么叫圆弧?直线就是从A往B走不拐弯不变向,圆弧就是按某种规则不断的变向走。所以,直线和圆弧的定义当中最为核心的就是两个字:方向。
我们先定义了直线就是从A往B走不拐弯不变向,再定义出长度的:从A往B走不拐弯不变向所走的路程就叫单位1。
可是,西方人说线是由无数个点组成的,这是术。这个术你之所以会接受,是因为你把如下知识给迁移过来了:在现实中你从A走到B,不管怎么走,你所走过的路径上都有一串脚印,脚印就是点,路径就是线,“线是由点组成的”你就接受了。
显而易见,在人的意识当中的“从A往B走不拐弯不变向的直线”跟“按某种规则不断的变向走的圆弧”这是两个东西,想把这两个东西联系起来就得在中间架一座桥。西方人说线是由无数个点组成的就是这座桥,这句话本身就是微积分。这座桥是虚构出来的,是不成立的。西方人把直线说成由无数个点组成,又把圆弧也说成由无数个点组成,这不就是今天在电脑 里面见到的马赛克吗?这个马赛克的本质不就是折线吗?直——折——曲。
当然,还有一种办法进行“巧妙”的转换,用物理学来描述:直线就是从A匀速走到B,这样路程即长度就变成了时间,时间可以测,时间没有直曲之分,“以时间换空间”。可是,圆弧该怎么来描述呢?圆弧就是从A做匀速圆周运动走到B。然而,匀速圆周运动的线速度公式是V=s/t=2πr/t,这不又拐回空间了吗?凭啥说k1=k2=π,仍然没有回答啊。
所以,折腾来折腾去,所求得的圆弧长度仍然只是一个逼近值。自己发明出一个“k1=k2=π”就是在强行架桥,强行把直和曲打通。
实际上,我们完全可以大大方方的承认所求只是逼近值,这也在直与曲之间架起了一座桥,这座桥在现实中是够用的。
唉,这个西方人吧,好比他先脱裤子放屁,人家就笑话他,他听完之后不是去改错反而去证明脱裤子放屁才是正确的,是必须的,这么做是为全人类负责。
注意,我并非是在否定“无限逼近”的价值,我只是在说,“无限逼近”不是“等于”,我只是在问,凭啥说k1=k2=π。
我之所以选用“直曲转换问题”为例子,这是因为:
一、数学中的直曲转换问题本身就很重要影响就极大,我们完全可以说现代数学大厦就是建立在k1=k2=π之上的。
二、换一个语境就成了“是非曲直”,曲指的作恶,直指的是行善。
我有理由相信,大家读过我的文章之后已经明白了骗术的“基本法则”就是:徐徐图之。他们并非是直接指鹿为马,而是通过“不断细分”这样的手法逐步“化直为曲”即一步一步的歪曲。
“不断细分”在现实中就是“多大点事啊,你这么咄咄逼人?”、“小题大做你干什么呀?”,在现实中就是“我是不小心的”、“我给你道个歉好吧,本来也没有多大的事”。通过这样的方式,一步一步的把你引上歧路把你带上贼船。
当然,你可能会说,这么多人都上了贼船,我也是没办法啊,我也得吃饭啊。嗯,是这样的,但你到底是“心曲”还是“腰曲”呢?这事只有你自己最清楚。如果你是“心曲”,你跟红衣教主就是一伙的,如果你是“腰曲”然而“心正”你就是身在曹营心在汉。
当然,你可能还会说,就算我是“腰曲”且“心正”那又如何呢?这么多人上了贼船,人类毁灭是迟早的事啊,我这么干除了能对得起自己的良心并没有什么实实在在的意义啊。说得好!所以是“身在曹营心在汉”,得有“汉”!“汉”是什么?“汉”就是不断发展,楼越盖越高,地基不牢的一定会崩塌的,狐狸尾巴一定是会露出来的。换言之,你仅仅是自己“腰曲”且“心正”确实是意义极有限的。
更为重要的是,红衣教主并不会因为一次、两次失败他就洗心革面了,恰好相反,红衣教主也是“自有接班人”的,上一个红衣教主败露了,下一任红衣教主就会总结“经验教训”,完善自己的骗术。具体怎么完善呢?还是那个招,“不断细分”,这次他会更“细”,否则为什么你今天能听到“细节里面有魔鬼”,否则为什么今天“精致生活”大流行?
可是,比上一代红衣教主做得更“细致”,更为“不断细分”,这就意味着总步数会增加,红衣教主得手的时间就会延后,简言之,他变慢了。红衣教主能忍得了吗?他是忍不了,因此怎么他会怎么办呢?既然总步数变多了,那就提高“效率”,以时间换空间。为什么今天你总在听人给你谈“效率”呢?就是这个道理。
这里面有一个“文字游戏”是需要重视的。下一代红衣教主总结上一代教主之所以失败就是太快,他的办法就是慢一点。而另一方面,下一代红衣教主总在宣讲“高效率”,要快一点,这难道不是自相矛盾吗?这一点都不矛盾,“慢”在此处的内涵指的更加细分,通过增加步数来完成欺骗之目的,并非你所认为的那个速度慢;“快”的内涵是因为增加了步数所以就得提速,这样总时间就不变。用同一个词汇去表达不同的内涵,这是很常见的,红衣教主利用了这一点,以达混淆视听之目的。
这样,正义一方的对策自然就是“慢慢来”,拒绝追求“高效率”。越是“慢慢来”,红衣教主就越是心急,因为他被拿住了要穴。红衣教主的办法自然就是大造声势,让多数人产生一种幻觉,若是自己不加快步伐就会被抛弃,否则为什么今天焦虑会如此的普遍?
正因为如此,正义一方的主要精力并非用在揭露红衣教主的骗术上面,而是用在加快发展步伐上面,这就意味着正义一方的战士们升级了。换言之,21世纪的今天,水平不够高你加入不了正义的阵营,或者你只能做一点外围的工作。用大白话来说,500年前作为一名正义战士你是一刀一个怪,今天你得是一刀两个怪。为什么李德胜会让人产生神仙下凡之感呢?就是这个道理。李德胜是“升级版本”,而许多人在还刻舟求剑,以古代来测量今天。
就说这么多吧。我得啰嗦一句,我只是在把事情讲清楚,并没有攻击人的意思,各位何去何从是自己看着办。
应该是斜边无限逼近圆弧段,而不是两直边之和逼近圆弧段
果然是你编号啊。
数学就是数学,数学和社会对上吗?相信数学和社会能对上才是被你“徐徐图之”了。本人作为西西河天才,要坚决揭露编号这种骗子行为,昭告天下!
虽然看不懂,但是编号老师一写就是一大篇,看上去挺厉害的样子,我读书少,不要骗我。
正好在知乎上看到一篇文章,给我的感觉也是这样,不知道编号老师有没有兴趣讲解一下。尼古拉·特斯拉真的那么强大吗?
尼古拉特斯拉留下的手稿,因为我研究河图洛书,所以这东西我一看就明白怎么回事。
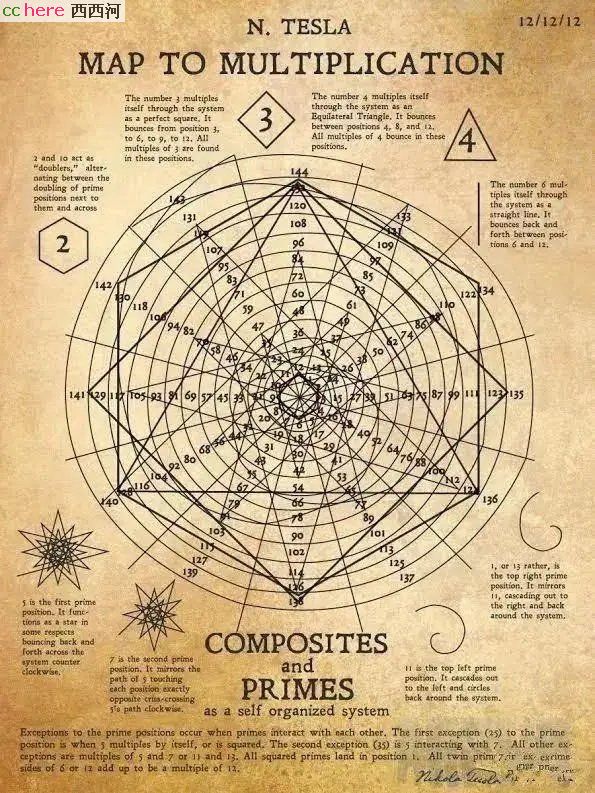
。。。
二、等角螺旋的等角?=0的时候,等角螺旋就会演化成直线
。。。
综上所述这就是一个无穷秩序的螺旋投影,而这个螺旋投影它是以旋涡的形态来呈现的,这就和基础物理解释的不一样了,基础物理解释引力的存在是因为离心力和向心力的作用,另外相对论对引力的解释在广义相对论定义是由于质量和能量引起的时空弯曲现象,但是特斯拉的手稿展现出来的螺旋投影,即投影旋涡就是一个层叠压缩模式,在上面是找不到质量和能量存在的,而是一种高密度的层叠压缩。就是说如果能与这种存在但不可定义的东西建立起共振的话,反重力能实现,所以我在特斯拉留下的手稿中又发现了这个(如下图)。
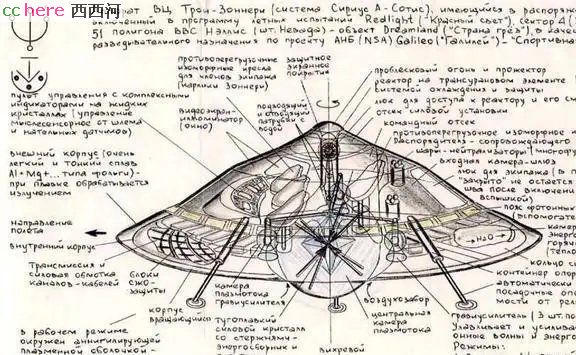
。。。
最后我发现数学旋涡和我国古代的河图洛书规则是一致的,这也是我看到这张图时为什么就能get到的原因。