主题:【翻译】计算机几何基础算法(一) -- 东方射日
作者 Ibackstrom
前言
就我所知,似乎不少程序员害怕几何问题,我想如果把几何问题从编程中剔除,他们一定很赞同。但不幸在绝大部分图形运算中,基本的几何知识是必不可少的。尤其在电脑游戏,你会到处遇到几何问题。在这里,我将试图介绍一些几何的基本概念和算法,让他们变得不那么可怕。
向量(Vector)
在几乎所有的几何问题中,向量(有时也称矢量)是一个基本点。向量的定义包含方向和一个数(长度)。在二维空间中,一个向量可以用一对x和y来表示。例如由点(1,3)到(5,1的向量可以用(4,-2)来表示。这里大家要特别注意,我这样说并不代表向量定义了起点和终点。向量仅仅定义方向和长度。
向量加法
向量也支持各种数学运算。最简单的就是加法。我们可以对两个向量相加,得到的仍然是一个向量。我们有:
V1(x1, y1)+V2(x2, y2)=V3(x1+x2, y1+y2)
下图表示了四个向量相加。注意就像普通的加法一样,相加的次序对结果没有影响(满足交换律),减法也是一样的。
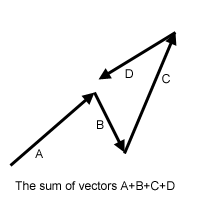
点乘(Dot Product)
如果说加法是凭直觉就可以知道的,另外还有一些运算就不是那么明显的,比如点乘和叉乘。
点乘比较简单,是相应元素的乘积的和:
V1( x1, y1) V2(x2, y2) = x1*x2 + y1*y2
注意结果不是一个向量,而是一个标量(Scalar)。点乘有什么用呢,我们有:
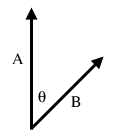
A B = |A||B|Cos(θ)
θ是向量A和向量B见的夹角。这里|A|我们称为向量A的模(norm),也就是A的长度, 在二维空间中就是|A| = sqrt(x2+y2)。这样我们就和容易计算两条线的夹角:
Cos(θ) = A B /(|A||B|)
当然你知道要用一下反余弦函数acos()啦。(回忆一下cos(90)=0 和cos(0) = 1还是有好处的,希望你没有忘记。)这可以告诉我们如果点乘的结果,简称点积,为0的话就表示这两个向量垂直。当两向量平行时,点积有最大值
另外,点乘运算不仅限于2维空间,他可以推广到任意维空间。(译注:不少人对量子力学中的高维空间无法理解,其实如果你不要试图在视觉上想象高维空间,而仅仅把它看成三维空间在数学上的推广,那么就好理解了)
叉乘(cross product)
相对于点乘,叉乘可能更有用吧。2维空间中的叉乘是:
V1(x1, y1) X V2(x2, y2) = x1y2 – y1x2
看起来像个标量,事实上叉乘的结果是个向量,方向在z轴上。上述结果是它的模。在二维空间里,让我们暂时忽略它的方向,将结果看成一个向量,那么这个结果类似于上述的点积,我们有:
A x B = |A||B|Sin(θ)
然而角度 θ和上面点乘的角度有一点点不同,他是有正负的,是指从A到B的角度。下图中 θ为负。
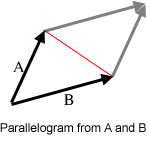
另外还有一个有用的特征那就是叉积的绝对值就是A和B为两边说形成的平行四边形的面积。也就是AB所包围三角形面积的两倍。在计算面积时,我们要经常用到叉积。
(译注:三维及以上的叉乘参看维基:http://en.wikipedia.org/wiki/Cross_product)
点-线距离
找出一个点和一条线间的距离是经常遇见的几何问题之一。假设给出三个点,A,B和C,你想找出点C到点A、B定出的直线间距离。第一步是找出A到B的向量AB和A到C的向量AC,现在我们用该两向量的叉积除以|AB|,这就是我们要找的的距离了(下图中的红线)。
d = (AB x AC)/|AB|
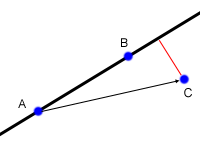
如果你有基础的高中几何知识,你就知道原因了。上一节我们知道(AB X AC)/2是三角形ABC的面积,这个三角形的底是|AB|,高就是C到AB的距离。有时叉积得到的是一个负值,这种情况下距离就是上述结果的绝对值。
当我们要找点到线段的距离时,情况变得稍稍复杂一些。这时线段与点的最短距离可能是点到线段的某一端点,而不是点到直线的垂线。例如上图中点C到线段AB的最短距离应该是线段BC。我们有集中不同的方法来判断这种特殊情况。第一种情况是计算点积AB Bc来判定两线段间夹角。如果点积大于等于零,那么表示AB到BC是在-90到90度间,也就是说C到AB的垂线在AB外,那么AB上到C距离最近的点就是B。同样,如果BAAC大于等于零,那么点A就是距离C最近的点。如果两者均小于零,那么距离最近的点就在线段AB中的莫一点。
源代码参考如下:
//Compute the dot product AB BC
int dot(int[] A, int[] B, int[] C){
AB = new int[2];
BC = new int[2];
AB[0] = B[0]-A[0];
AB[1] = B[1]-A[1];
BC[0] = C[0]-B[0];
BC[1] = C[1]-B[1];
int dot = AB[0] * BC[0] + AB[1] * BC[1];
return dot;
}
//Compute the cross product AB x AC
int cross(int[] A, int[] B, int[] C){
AB = new int[2];
AC = new int[2];
AB[0] = B[0]-A[0];
AB[1] = B[1]-A[1];
AC[0] = C[0]-A[0];
AC[1] = C[1]-A[1];
int cross = AB[0] * AC[1] - AB[1] * AC[0];
return cross;
}
//Compute the distance from A to B
double distance(int[] A, int[] B){
int d1 = A[0] - B[0];
int d2 = A[1] - B[1];
return sqrt(d1*d1+d2*d2);
}
//Compute the distance from AB to C
//if isSegment is true, AB is a segment, not a line.
double linePointDist(int[] A, int[] B, int[] C, boolean isSegment){
double dist = cross(A,B,C) / distance(A,B);
if(isSegment){
int dot1 = dot(A,B,C);
if(dot1 > 0)return distance(B,C);
int dot2 = dot(B,A,C);
if(dot2 > 0)return distance(A,C);
}
return abs(dist);
}
上面的代码看起来似乎是很繁琐。不过我们可以看看在C++和C#中,采用了运算符重载的类point,用‘*’代表点乘,用'^'代表叉乘(当然'+''-'还是你所希望的),那么看起来就简单些,代码如下:
//Compute the distance from AB to C
//if isSegment is true, AB is a segment, not a line.
double linePointDist(point A, point B, point C, bool isSegment){
double dist = ((B-A)^(C-A)) / sqrt((B-A)*(B-A));
if(isSegment){
int dot1 = (C-B)*(B-A);
if(dot1 > 0)return sqrt((B-C)*(B-C));
int dot2 = (C-A)*(A-B);
if(dot2 > 0)return sqrt((A-C)*(A-C));
}
return abs(dist);
}
运算符重载不在本文讨论中,不过如果你是C++或C#的程序员,而你却不确定如何重载运算符的话,我建议你赶快找本书,然后最好自己写一个包含运算符重载的类point。这样一个类会让很多几何问题简单许多。
本帖一共被 1 帖 引用 (帖内工具实现)
多边形的面积
另外有一个普遍的问题是计算一个给出各个顶点的多边形的面积。我们考虑如下图所示的有五个顶点的非凸多边形。要计算它的面积,我们可以将它分割为一个个三角形。在这个五边形中,我们可以分割为三个三角形:ABC,ACD和ADE。不过,等等....你可能会反对,并不是每个三角形都是这个五边形的一部分。这里,叉积是有正负的优势就大大体现出来了,它会让每件事情都变得很奇妙。首先,我们计算ABxBC可以得到三角形ABC的面积,如果你还记得右手法则的话,在本例中,AB到BC是顺时针,那么我们就会得到一个负值。同样地,由ACxAD的叉积我们可以得到三角形ACD的面积,这也是一个负值。最后,我们计算ADxAE,由于ADE三点是逆时针方向,我们知道那将得到一个正值。我们将这三个面积(两负一正)相加,本例中,我们就得到一个负值,那个绝对值就是这个多边形的面积。
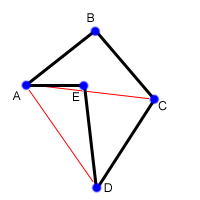
看上图,很显然多边形的面积就是三角形ABC和ACD的面积之和减去三角形ADE的面积。
最后一点提示,如果我们计算的面积是负值,表示各个顶点是按顺时针方向给出的。
下面给一段具体的代码,其中顶点是以2维数组的方式给出:
int area = 0;
int N = lengthof(p);
//We will triangulate the polygon
//into triangles with points p[0],p[i],p[i+1]
for(int i = 1; i+1<N; i++){
int x1 = p[i][0] - p[0][0];
int y1 = p[i][1] - p[0][1];
int x2 = p[i+1][0] - p[0][0];
int y2 = p[i+1][1] - p[0][1];
int cross = x1*y2 - x2*y1;
area += cross;
}
return abs(cross/2.0);
注意,如果各顶点都是整数,最后的面积是一个整数的一半。(0.5的整数倍)
线-线交点
你将发现寻找两条线的交点是最普遍的几何问题之一。尽管这个问题很普遍且看起来很简单,但是还是有许多程序员感到无从下手。第一个问题是直线是以什么形式给出的?或者说你希望它是什么形式?理想情况下,每条线都可以写成Ax+By=C的形式。ABC这三个值就可以唯一确定一条直线。然而,经常给我们的直线并不是这样的形式,不过我们总可以很容易地将两个点装换成这种标准形式。例如给出直线上两个点(x1,y1)和(x2,y2),我们可以等到相应的A,B和C:
A = y2-y1
B = x1-x2
C = A*x1+B*y1
无论直线是如何描述的,我们总可以有直线上的至少两个点,然后以上述方式得到A,B和C。好现在我们可以假定我们有两条直线:
A1x + B1y = C1 (一)
A2x + B2y = C2 (二)
那么要找这两条直线的交点就变成一个简单的二元一次方程问题。
double det = A1*B2 - A2*B1
if(det == 0){
//Lines are parallel
}else{
double x = (B2*C1 - B1*C2)/det
double y = (A1*C2 - A2*C1)/det
}
复习一下初中数学,将(一)两边乘以B2,(二)两边乘以B1,然后将两式相减得到:
A1B2x - A2B1x = B2C1 - B1C2
那么就得到 x = (B2C1 - B1C2 )/(A1B2 – A2B1) 类似第你可以得到y.
现在你就得到了两条直线的交点。那么在两条线段的情况下又怎样呢?你需要确认我们的到的点在两条线段上。如果线段的两个端点是(x1,y1)和(x2,y2),那么你只要检查min(x1,x2) ≤ x ≤ max(x1,x2) 和min(y1,y2) ≤ y ≤ max(y1,y2)就可以认为该点在线段上。这里特别提醒一下浮点数的精度问题。如果交点正好在线段的端点或线段是水平/垂直的,简单的比较是可能有问题的。这里你可以定义一个最小的许可误差或是用一个分数的类来进行。
三点确定一个圆
给出不共线的三个点就可以唯一确定一个圆。但这个圆的圆心和半径是多少呢?这个问题实际上就是求直线交点的一个简单应用。如下图示,我们首先确定XY和YZ的中垂线,他们的交点就是圆心。
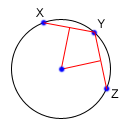
要得到XY的中垂线,首先我们可以有上面的介绍得到XY的直线Ax+By=C。那么它的中垂线就是 -Bx+Ay=D。至于D是多少,可以代入XY的中点得到。中点简单的就是XY两点的x和y坐标的平均值。同样,我们可以得到YZ的中垂线。再用上面介绍的方法得到交点,那就是圆心。
镜像
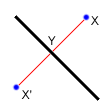
找到一个点关于一条直线的镜像,我们可以采用上面三点确定一个圆同样的技巧。首先注意到点X和镜像点X'到直线的距离相等,同时注意到XX'垂直于所给的直线。那么如果所给出的直线是Ax+By=C,我们已经知道它的垂线是-Bx+Ay=D。代入点X,就可以计算出D。现在我们可以计算这两直线的交点Y。那么X'=Y-(X-Y)
旋转
旋转并不完全和计算直线的交点相关。但是我觉得把它和镜像问题放在一起还是有好处的。事实上找到镜像点的另一种方法是将点X相对点Y旋转180度。
想象一下将一点相对另一点逆时针旋转角度θ 。简单话我们可以假设相对原点旋转,我们有x' = x Cos(θ) - y Sin(θ) 和 y' = x Sin(θ) + y Cos(θ) 。如果相对其他点旋转,那么只要将坐标平移使该点为原点,然后采用以上公式计算,接着再将坐标平移回去即可。
本帖一共被 2 帖 引用 (帖内工具实现)
凸包
对于一组点,能将所有点包含在内的最小的凸多边形就是所谓的凸包。这个凸包是有该组点中的若干点组成的。可以想象这些点是一块板上钉的钉子,用一个弹性很好的橡皮筋箍住所有的点,那么这条橡皮筋所形成的多边形就是凸包。有很多种不同的算法可以计算凸包,本文中,我们将讨论其中一种算法,该算法在大多数情况下的性能足够好,但是比起其他一些算法还是相当慢的。
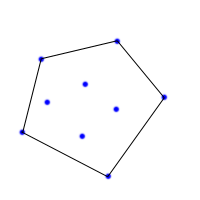
首先,我们可以遍历所有点,找到最左边的点(x最小),如果有两个以上的点的x相同,那么我们取最高的那个点(y最大)。显然该点必然是凸包上的一个点,我们就设该点P为起点。现在我们以顺时针方向遍历所有的点。这里我们要使用叉乘算子。如何确定哪一个点是下一个点呢?我们可以任选一个未用的点N作为下一个点,然后遍历所有其他未用的点,假设是X。如果(X-P) x (N-P) 是负的,我们将X设为新的下一个点N。在我们遍历所有点后,得到的点N就是凸包上的下一个点。下面的图示表明了该算法的步骤:
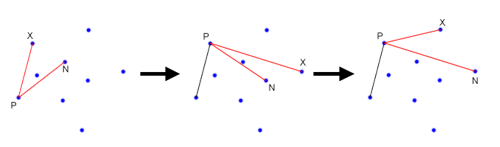
接着同样的方法我们可以找到凸包的下一个点,直到我们返回起点。
这里我们是使用叉乘寻找顺时针的下一个点是很容易理解的。不过在有几点共线的时候,事情稍稍有点复杂。假设不考虑共线的情况,代码很简单:
convexHull(point[] X){
int N = lengthof(X);
int p = 0;
//First find the leftmost point
for(int i = 1; i<N; i++){
if(X[i] < X[p])
p = i;
}
int start = p;
do{
int n = -1;
for(int i = 0; i<N; i++){
//Don't go back to the same point you came from
if(i == p)continue;
//If there is no N yet, set it to i
if(n == -1)n = i;
int cross = (X[i] - X[p]) x (X[n] - X[p]);
if(cross < 0){
//As described above, set N=X
n = i;
}
}
p = n;
}while(start!=p);
}
如果考虑共线的情况,代码稍微复杂一些。首先我们添加一个bool型的参数,该参数指定线上的点是否记为凸包上的点。
//If onEdge is true, use as many points as possible for
//the convex hull, otherwise as few as possible.
convexHull(point[] X, boolean onEdge){
int N = lengthof(X);
int p = 0;
boolean[] used = new boolean[N];
//First find the leftmost point
for(int i = 1; i<N; i++){
if(X[i] < X[p])
p = i;
}
int start = p;
do{
int n = -1;
int dist = onEdge?INF:0;
for(int i = 0; i<N; i++){
//X[i] is the X in the discussion
//Don't go back to the same point you came from
if(i==p)continue;
//Don't go to a visited point
if(used[i])continue;
//If there is no N yet, set it to X
if(n == -1)n = i;
int cross = (X[i] - X[p]) x (X[n] - X[p]);
//d is the distance from P to X
int d = (X[i] - X[p]) (X[i] - X[p]);
if(cross < 0){
//As described above, set N=X
n = i;
dist = d;
}else if(cross == 0){
//In this case, both N and X are in the
//same direction. If onEdge is true, pick the
//closest one, otherwise pick the farthest one.
if(onEdge && d < dist){
dist = d;
n = i;
}else if(!onEdge && d > dist){
dist = d;
n = i;
}
}
}
p = n;
used[p] = true;
}while(start!=p);
}
(译注:该算法复杂度为O(N^2),有更好的算法,复杂度为O(NLogN),参见维基:
http://zh.wikipedia.org/w/index.php?title=%E5%87%B8%E5%8C%85&variant=zh-cn
http://en.wikipedia.org/wiki/Convex_hull_algorithms
多边形内点
给出一个任意多边形的顶点和一个点,测试该点是否在多边形内、外或边上。
这个问题可以简单使用线-线交点和点-线距离的算法。
首先我们可以使用点-线距离来测试该点是否在边上。如果该点到任意一条边的距离为0,那么显然是在边上。
然后,我们要检测该点是否在多边形内部。想象一下以该点为起点,向任意方向画一条射线,每一次该射线和边相交,该射线就由多边形内部穿越到外部或相反。这样,如果该点在多变形内部,该射线必然和边相交奇数次。技术上我们不需要真的画一条无限长的射线,我们只要有一足够长的线段即可。如果另一端点没有选好,你有时会陷入困境,例如线段两点均在多边形内部或和某一条边重合。简单但是龌龊的做法是用一个足够大随机数作为线段的另一个端点,这个方法虽然不优美且不安全,但是在实践中它管用。这线段和某一条边重合的概率是如此之小以至于你可以拍胸脯说可以得到正确的解答。如果你还是不放心,你可以选几个随机点,然后返回最普遍的答案。
String testPoint(verts, x, y){
int N = lengthof(verts);
int cnt = 0;
double x2 = random()*1000+1000;
double y2 = random()*1000+1000;
for(int i = 0; i<N; i++){
if(distPointToSegment(verts[i],verts[(i+1)%N],x,y) == 0)
return "BOUNDARY";
if(segmentsIntersect((verts[i],verts[(i+1)%N],{x,y},{x2,y2}))
cnt++;
}
if(cnt%2 == 0)return "EXTERIOR";
else return "INTERIOR";
}
本帖一共被 1 帖 引用 (帖内工具实现)
鲜花已经成功送出。
此次送花为【有效送花赞扬,涨乐善、声望】
楼主若是有这个闲情,普及一下渲染技术?
今天在你这里开了荤
谢谢:作者意外获得【通宝】一枚
鲜花已经成功送出。
此次送花为【有效送花赞扬,涨乐善、声望】
比如判断某点是否在一条直线上,如果是考虑点到线的距离,计算机不可能算到正好是0,而可能是1.0E-10这样的数。
还有判断点是否处于多边形内的这样问题,一旦存在比较计算数值是否相等,就会受计算精度的影响。如果不注意,很容易出现一系列错误。
在(二)中,线-线交点一节中简单提到了浮点数的精度问题:
是topcoder上的一个高人的网名吧
具体可以看我前篇翻译的前言: