主题：【原创】数理逻辑发展的简单脉络（1） -- 泰让

弗雷格和一阶谓词演算

弗雷格

继布尔之后，美国学者皮尔斯和德国学者施罗德又分别对命题演算做了补充。1879年，德国数学家弗雷格发表了《概念文字》（Begriffsschrift）。在这本论文中，弗雷格总结了命题演算的最新成就，完善了“谓词”和“量词”的概念，并进一步地建立了一阶谓词演算体系。

所谓谓词，可以简单看作逻辑领域内的函数，不同的是函数把数（或者几个数）转化成数，而谓词的值域则是真或者假。举个简单的例子，如果谓词P(x)表示“x是白色的”这个命题，那么我们可以用：P(雪）=真，P(棉花）=真，P(煤球）=假

来表达 雪是白色的，棉花是白色的，煤球不是白色的 这三个命题。

而所谓量词，则是指在命题前修饰范围的词。这个概念本身其实并不新鲜，我们看到亚里士多德的4种基本命题中，已经有了“所有”“某些”这些概念。弗雷格将其同命题本身分离开来，用专门的记号表示“所有”和“存在”这两个概念。在现代记号中，我们一般用倒过来的A和E表示。如果我们仍用P(x)表示x是白色的，而用集合X表示“所有绵羊构成的集合”，那么

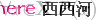
翻译成日常语言，就是“所有的绵羊都是白色”，而

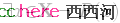
则表示，“存在某不是白色的绵羊”。可以看出，这两个命题是相对的。

有了量词和谓词这两个工具后，逻辑的表达能力前进了一大步。但弗雷格的贡献不仅限于此，更有意义的是，他在《概念文字》一文中，建立了一整套的一阶谓词演算系统，其中包含有若干条推理规则，作为不证自明的公理。这些公理构造出了第一个关于推理本身的公理化系统。一阶谓词演算和布尔等人建立的命题演算，仍然是现在大学里初等数理逻辑课程的主要核心内容。

皮亚诺和公理化算数系统

皮亚诺

与逻辑学的稳步发展相比，数学，特别是数学分析在18、19世纪的发展可以说是突飞猛进。然而与这种飞速的进步不相适应的是，分析学的基础远非稳固。事实上，许多很基本的概念，比如函数的连续，可微，以及级数的收敛都没有严格的定义。我们现在初学微积分接触到的“德尔塔-艾普西隆”表达法其实是很后来才出现的。在这之前，即使如柯西这样的大牛，也会时不时的犯错误，证出个乌龙定理什么的。这样不严格的基础显然会限制分析的发展。德国数学家维尔斯特拉斯首先做了这方面的工作。随着对分析基础严格化工作的进展，人们逐渐发现，即使是对实数这种概念，仍然缺乏严格的定义。

1874年，德国数学家康托发表论文，建立了朴素集合论，这是个非常好用的数学工具。许多数学概念由此得以比较好的描述。用集合论的办法，戴德金分割可以用端点为有理数的相互嵌套的集合区间来描述实数。而有理数则是可以由自然数来定义的。这样一来，所有的基础都建立在了自然数上了。那么刨根问底的话，自然数又是什么呢？

意大利数学家皮亚诺对这个问题给了一个答案，他的想法是，可以用形式化逻辑这个工具来描述自然数。他用几条公理定义了自然数的概念。这是逻辑学在数学上的一次成功运用，也给“数理逻辑”这个词提供了新的涵义，在布尔等人的时代，人们试图用数学描述逻辑，而皮亚诺则开始用逻辑构建数学基础。自此以后，数学基础，以及集合论都被视为数理逻辑的分支学科。

同弗雷格一样，皮亚诺也独立地建立了一套带量词逻辑演算系统，但表述不如弗雷格严谨。不过他用的符号更为实用（弗雷格使用一套类似于现在数据结构的树一样的二维记号，不利于书写），现在我们用的属于，包含等集合符号，都来自于他。皮亚诺的另一个贡献是教学方面的成就，他和他的学生Burali-Forti, Padoa, 和Pieri都有相当成就，组成了逻辑学中的意大利学派。