主题:【原创】茗谈201:海上余绪 -- 本嘉明
按照北京大学数学科学学院范后宏教授在“古今数学思想”课:
至此,我们终于可以引入Hilbert大神对直线的理解了:点和直线不可定义,真正需要的是点和直线之间的关系!而对于点和直线之间的最基本关系,Hilbert用公理来确定。“几何学就是给直线一个定义”,只要给出一个直线的定义,就有一套几何学!(这里说的给直线一个定义,意思就是给出一个与现有数学体系无矛盾的描述直线和点之间关系的公理)。
范教授认为有物理信仰的人定义直线为光子走过的路径, 这个倒是符合人的直觉。但是光经过有质量的物体会发生弯曲。非欧几何不仅仅在逻辑上是存在的,它更是真实世界的几何学!到头来我们才发现,原来我们一直以为很显然的初中学的欧几里得几何学,充其量只是数学家头脑中凭空构造出来的玩具而已。。。
最后在小尺度上光子因为量子效应不再具有很好的粒子性,不再具有通常意义上的轨迹,因此,在小尺度上(小到量子效应很明显),几何学根本就是不存在的!这也就是为什么量子力学中就再也没有轨迹这种几何学概念了。
几何从产生到灭亡,呜呼。。。。。。
古人跟初中生没必要搞得那么复杂
几何原本的对象原本是直观的实体,即便是抽象也必须有具体的图像。而不是我们现在理解的抽象的抽象。亚里士多德最明显
亚里士多德的定义是「连结两点的直线」。按照文本中用来举例直线的例子,比如地平线、水面和光,那么来源很清晰了。需要注意的是,希腊人说的直线都是线段,而不是我们所理解的可以无限长的直线。这也是自然主义直观理解的明证。
而不是0
一个小错,纠正一下。
规范场建立在微分几何基础上
黎曼几何是微分几何的子集。
凝聚态物理现在研究各种拓扑的物质等等。
所谓直线其实就是曲面上的测地线
直线的特殊性在于它是处于曲率为0的曲面(即平面)上的测地线。
这里不存在任何的理论冲突,以及理论难题。
西方自从毕达哥拉斯学派开始对于数学就有一个深深的敬仰。
毕达哥拉斯学派认为任何物体任何数都可以等分,认为这是一种宇宙的秩序,然后有人发现了无理数,严重挑战了这个信仰,于是那人被处死了。
欧几里得的几何原本的后半部分现在看来几乎完全没用,就是他们不承认无理数,然后在只存在有理数的假设的基础上推演了一大堆的结论。
不要用实用主义者的眼光去看那些奥秘探寻者,或者说寻道者,人家不会这么犬儒。
否则勾股定理为啥需要证明?
从实用角度证明不证明有区别吗?
三角形内角和都是180度,为啥要证明,量角器量几次都一样,用于生产就已经够了。
不过,数学我可不敢跟你杠了哈😅😅😅
别忘了,你已经加入了气人宗,有组织可以依靠。
教主是要证明黎曼猜想的,能否成功我不知道,但我知道,我那点数学知识,哪敢跟教主杠啊!😅😅😅
威名远播,其惊世骇俗的光辉事迹和言论,我岂能不知?好歹我也算是一名老河友好吧?虽然中间因为拔插头和翻墙等各种因素不得已而短暂上过岸,但还不至于如此孤陋寡闻,我内心深处,其实也一直对教主是高山仰止景行行止的,但自从上次看到你和月之回忆河友的创纪录多层级友好和谐交流探讨后,对于你出面来挑战教主的天威,我还是比较看好的,加油!
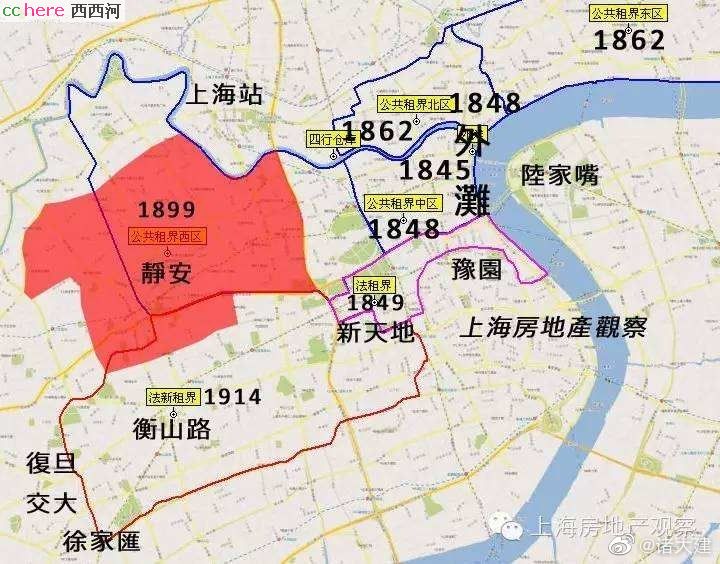
上海人拍的《爱情神话》,广受上海人好评,恰恰说明上海相当一部分人,即使不是主流,还活在殖民地历史里,丝毫不以为耻,反以为荣。上海的海派文化的“海”,应该是上海的海,而不是舶来的殖民地文化的那个海。上海和香港,应该同步进行去殖民地意识,时间会冲刷干净上海的殖民地意识。
- 待认可未通过。偏要看
没别的;他这几年对中国国力“霸兵”式的长起来没啥概念;对赵立坚的粗口不适应,以TG的行事风格,我能保证锤死你的时候才出手整你心里是不忿的;有这种问题的,不只是本大一个人;是很多;推上,油管上太多了;
复旦大学主校区在杨浦区邯郸路220号,和交大是南北对角线。
复旦大学初建时借用了李鸿章的祠堂办学。在现在的华山路,倒是和交大挨得近。但很快就搬走。李鸿章祠堂成为复旦中学校址(但不是复旦附中,两所学校😁)。