主题:一道比较难的数独题,至少我是花了好几天工夫才做出来 -- kmy1810
下面是只应用基本三原则(如果某格子所在行、列、块内有已经确定的值,则将该值从待选队列中删除)的计算结果
注意右下角红色部分
97431 987431 871 8743 5 8743 8763 71 2
754321 875431 87521 8743 6 8743 873 71 9
764 2 76 8764 974 98764 5 3 1
7653 753 765 7653 732 1 4 9 8
8 5431 9 543 43 543 2 6 7
976521 9751 76521 76531 8 97653 97 752 4
9752 9875 3 754 974 9754 1 752 6
97651 9751 4 2 97 9765 97 8 3
以下为应用了基本三原则 + Naked Pair 规则的计算结果
97431 987431 871 8743 5 8743 6 71 2
754321 875431 87521 8743 6 8743 83 71 9
764 2 76 8764 974 98764 5 3 1
7653 753 765 7653 732 1 4 9 8
8 5431 9 543 43 543 2 6 7
976521 9751 76521 76531 8 97653 97 52 4
9752 9875 3 754 974 9754 1 52 6
651 51 4 2 97 65 97 8 3
earthcolor已把中下那块的第一行做出来了(1、8、3),但你的显然没有。
基本三原则 + Naked Pair还是没有充分利用所有的已知条件/结果。比如中下块,你的结果是:
76531 8 97653
754 974 9754
2 97 65
用Naked Single可以确定1只能在左上角。剩下的是:
1 8 97653
754 974 9754
2 97 65
再用一次Naked Single,3只能在右上角。这样得到:
1 8 3
754 974 9754
2 97 65
再用一次Naked Single,6只能在右下角:
1 8 3
754 974 9754
2 97 6
这一块的5只能在中间一行。用这个确定条件和Pointing Pair可以确定右下块里5和2的位置。
上面的计算只看了中下、右下两块。如果你用这个结果再排除其他块里的一些可能,你应该可你得出earthcolor的结果。
只有基本三原则是不够滴。
基本三原则自然是最基本的,Naked single,pointing pair这些是在一些特殊组合中基本三原则的简化/归纳,他们都是从基本三原则中推导出来的。
我做到这一步,然后再也想不出来还有什么可以往里填了。下面必须开始猜了么?
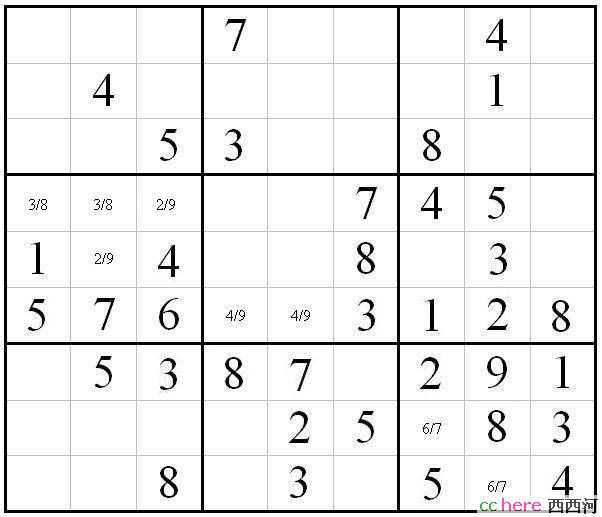
中中大格 最后一行为49或94
已经把结果更新了,可是仍然不知道该如何继续
我一边看着电视一边做,大约不到一个钟头做出来的。不是我聪明,而是碰巧了。
有时候,钻进了死胡同,自己把自己绕糊涂了,就不容易做。记得有一次作题,做一个标为中等难度的,费了好半天劲,大约好几天才做出来,我怀疑难度标错了。谁知同样的题,水平不如我的人不到半个小时就作完了。
邪门,不是吗?
因为这一行还差3、4、6三个数字,而该格所在的列已有4、6,只能填3。
已经更新了已有的结果
先说仅有两种可能的
(7,1)表示第七行第一列,下同
(7,1)和(7,6)都是4/6
(3,8)也是6/7
(4,3)和(5,2)都是2/9
(4,9)是6/9
(4,1)和(4,2)都是3/8
下一个关键的:
(1,2)也是3/8
又无法断定它到底是3还是8。
还请提示一下下面的思路吧。这道题花费了我几乎全部的元旦假期了,真是费神哪。
而不是一个小格的两种选择。
例如中间一行中间的大格,其最下面一行的第一第二格是49或者94。所以,这个大格里面的4和9这两个数字的位置其实比较确定了。
已经更新了partial solution
每个小的单元格有三个坐标,分别属于行列和九宫格三个维度,如果我们把图旋转九十度可以发现行列互换了,相当于交换了行列坐标,而如果交换每个格子的列坐标和九宫格坐标,所得的解也是一样的。
因此,不要拘泥于“标注的是一个大格里面的数字的可能性”,我所说的就是标注每个小单元的所有可能性,当然首先列出的是只有两种可能的,这样比较简单清楚。
例如(7,1)和(7,6)都是4/6,就是一行中的数字的可能性,和九宫格里的分布是等价的,也就是说这一行里面的4和6这两个数字的位置比较确定了。
(3,8)的6/7和(9,8)的6/7也是一样。
对于比较简单的题目,分而治之是个不错的方案,但对于较复杂的,就要综合分析行列九宫格共同的制约而不仅仅是一个大格里面数字的可能性了。
一般性的思路
1标注各单元可能数字
2约简
3查看各行列九宫格中各个数字可能出现的位置数
4以上方法都无效时,选择信息量最丰富的单元尝试(一般是牵一发而动全身的点)例如(9,8),(3,8),(8,7)等等互相关联的点。直到发现错误或找到答案。