主题：【原创】中国古代的科学家们——数学家之杨辉 -- 安德的游戏
杨辉是中国南宋的数学家，生于公元1238年，卒于公元1298年。杨辉是一位多产的作家，他的数学著作有《详解九章算经》12卷、《日用算法》2卷、《乘除通变算宝》3卷、《田亩比类乘除捷法》2卷、《续古摘奇算法》2卷及《九章算法篡类》等。他的著作中收录了不少现已失传的算题和算法，对于现在了解古代尤其是宋朝的数学成果起了很大的作用。应该说杨辉在数学上自己独创性的贡献并不多，但是对于前人数学成果的整理和研究的工作做得非常出色。
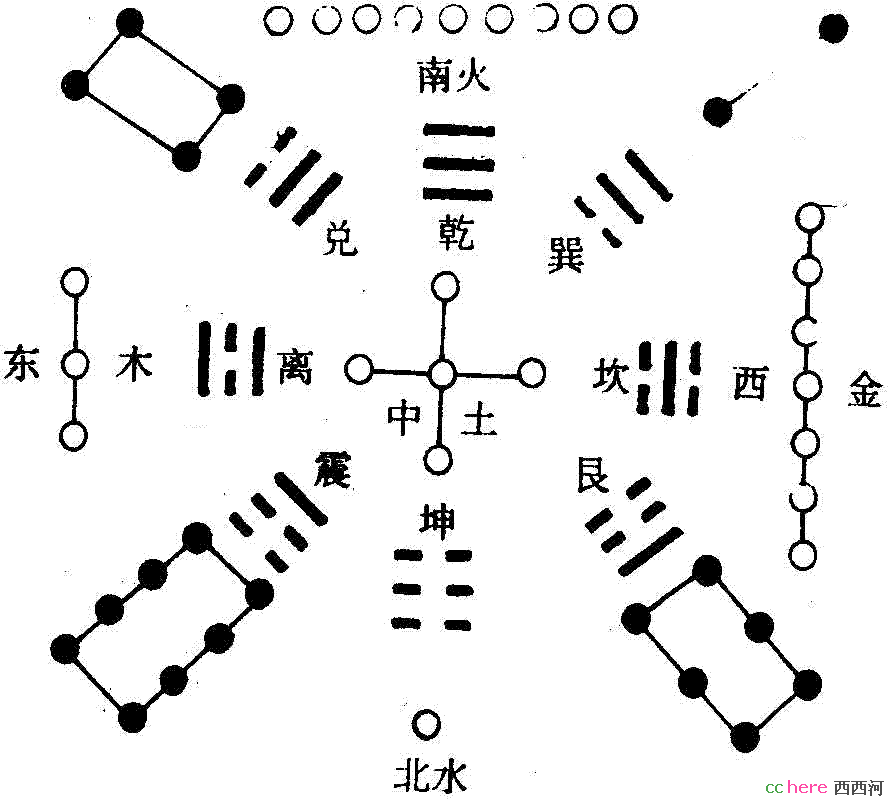
大家认识杨辉的名字，基本上都是从“杨辉三角形”上来的。其实，所谓的“杨辉三角形”，并不是杨辉首创，而是北宋的贾宪在他的著作《黄帝九章算经细草》中提出的。此书成于约公元1050年，其中的“开方做法本源图”就是杨辉三角形的原型，所以也被称为“贾宪三角形”。这个三角形的每一行，对应的是二项式(a+b)^n展开的系数。在这一方面，中国又比西方领先了差不多六个世纪。
杨辉在数学上的另一个重要的贡献是提出了幻方的构造方法。所谓的幻方，就是指在NxN的格子中填入1到N平方的自然数，使每一行每一列的和都相等。三阶幻方是最简单的幻方，又叫九宫图或者洛书，它的样子是
或者写成数字的形式，就是：
四 九 二
三 五 七
八 一 六
还有一个口诀：“二四为肩、六八为足、左三右七、戴九履一、五居中央。”传说是黄帝时代，洛水中浮起一只大龟，背上刻着这样的图案。洛书配上八卦，被用在风水学上，被称为洛书轨迹，用在奇门遁甲中，则形成了“休死伤杜开惊生景”八门。诸葛亮最擅长的八阵图就是源于此。
杨辉收集整理了很多不同阶的幻方，称其为“纵横图”，并写到了自己的著作《续古摘奇算法》一书中，可以说是世界上第一个给出如此多的幻方并讨论了它们的组成规律的数学家。
幻方的构造可以按照一个固定的规律，按奇数阶和偶数阶的不同，构造的方法也不一样。奇数阶的很容易。首先从最后一行的中间开始填起，从一开始递增，向斜下方延伸。如果超出了边界，就从相对边的位置继续。如果遇上已经填过的格子，就从填过的格子上方的格子继续。大家可以对照三阶幻方来看出这个规律。对于偶数阶幻方，如果是四的倍数，很容易，只要首先把从1到N平方的数字先按照行的方向填好，变成下面的样子：
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
然后除了对角线上面的数字不动以外，其他的数字跟中心对称位置的数字对调：
1 15 14 4
12 6 7 9
8 10 11 5
13 3 2 16
这样就构造好了。对于阶数是4m+2的幻方，构造的方法比较复杂。不过步骤是先构造好中心的幻方，然后在周围加上一圈数字就可以了。
杨辉的其他数学成就还包括，研究了“垛积问题”，也就是高阶等差级数的问题；创立“九归”口诀，介绍筹算乘除的各种快速算法；研究任意高次幂的开放运算和高次方程求解等等。由于他在数学上的杰出成就，和秦九韶，李冶，朱世杰一起并称为“宋元数学四大家”。
本帖一共被 1 帖 引用 (帖内工具实现)
恭喜：意外获得【西西河通宝】一枚
谢谢：作者意外获得【西西河通宝】一枚
鲜花已经成功送出。
此次送花为【有效送花赞扬，涨乐善、声望】
后来便还给老师了。看来我们祖先的数学成就很厉害呀。
“八阵图”已经失传了，当然也不是没有可能是从八卦图推演得来，不过如果真是这样，那我想诸葛亮一定要有外星人的智商水平......
据说唐李靖的六花阵法颇得武侯真味，可惜这个阵法也失传了（至少是记载在兵法书上的失传了，现实中有没有传承不敢说）。这里的疑点是，蜀汉以步兵为主，八阵图应该是步兵战术，而李靖所率概为轻骑，六花阵法应该是步骑协同战术，想来即便有所传承，李靖的原创成分也应该是相当大的。此外，按照史书记载，诸葛亮造刀，造连弩，都是为了练阵法（这是我所知道的最早的为战术想定设计和制造兵器），而到了唐朝，连弩大概已经失传了吧，那么八阵图没有了兵器的支持，效用如何恐怕很难说。
没有文献，瞎说说。我想主要是现在没什么人懂术数。洛书中的数如何演化出奇门遁甲中的局，没研究过，也说不出什么。也许遁甲局穷尽了各变量的状态，演化出阵法未尝不可。
至于八卦，别的不说，最基本的，它可以代表八个方位。上面那个图至少可以看出方位和数的结合。而数又可以表现为人数，火力配置等等。一个阵法（算法）的粗糙轮廓已经可见。