主题:【原创】中国古代的科学家们——数学家之祖冲之 -- 安德的游戏
- 共: 💬 38 🌺 66
中国古代的科学发展一直走在世界的前列,在很多领域的发现比西方要早一千多年。看一看古代科学家们的事迹,并不是要我们自大于古代的伟大成就,而是有助于我们我们学习他们的刻苦精神,以期创造未来的辉煌。
我先从数学家讲起,也许是因为中国古代数学的成就特别突出吧。
要说到数学家,大家最先想到的大概就是祖冲之和他的圆周率了。祖冲之是南北朝时期的数学家,生卒年是公元427-500年。祖冲之所以知名,是因为他把圆周率计算的精确度大大提高,西方一直到一千多年以后,才得到了精度更高的结果。其实说起来,祖冲之在计算圆周率的方法上没有很大的创新,沿用的是刘徽的割圆法。只不过刘徽计算到了圆内接3072边形,而祖冲之进一步加倍了多边形的边数,直到最后计算了24576边形的边长。
但是祖冲之在圆周率上的突出贡献是提出了两个圆周率的近似分数表示法,一个是疏率22/7,另一个是密率355/113。其中密率和圆周率真值之间的误差小于百万分之一,在分子分母小于1000以内的分数中,再没有其他的分数能够做到比这个比值更精确的了。现在还不知道祖冲之究竟是如何得到的这个结果。
其实别的不说,在计算的圆周率的过程中,要处理高达九位有效数字的运算,中间结果需要有十七、八位的精度要求,这是需要有多大耐心、恒心以及细心的工作呀。尤其是当时没有纸笔,没有我们现在做运算用的阿拉伯数字,而算盘一直到宋代才有,所以所有的计算是用小棍做的算筹来进行的。
这里对算筹多解释一点。算筹是用小棍来表示数目的。一根直放的小棍表示一,两根表示二,以此类推。等到了十,就把小棍横过来摆。所以二十三就是两个横棍子和三根竖棍子。到了百,就再竖过来,千就再横过来,以此类推交替。这样运算的时候就要特别小心,否则摆错了位置运算就全都错了。
可以想象,祖冲之用这种原始的计算方法,计算加减乘甚至开方的运算需要多么仔细和多大的耐心。在计算的过程中,祖冲之的儿子祖暅也参与进来,给了祖冲之很大的帮助。这里要特别说明一点的祖暅也是一位伟大的数学家,他提出的计算体积的“祖暅原理”也是一直到1000年以后才才由意大利数学家卡瓦列利提出。而祖暅运用这一原理正确推导出了球体积的计算公式。
祖冲之父子的研究成果,汇集在一部叫做《缀术》的书中,成为隋唐时期学习数学的十部课本之一。只可惜此书后来到了宋朝就失传了。
同时,祖冲之还是一位天文学家,关于他在天文学方面的成就,要等到和其他天文学家一起来讲了。为纪念这位伟大的古代科学家,人们将月球背面的一座环形山命名为“祖冲之环形山”,将小行星1888命名为“祖冲之小行星”。
本帖一共被 1 帖 引用 (帖内工具实现)
挑个小刺--纸和比当时是有的,不过没用来做数学运算。
有个趣闻,民国某年,当时都是各个大学自己出题让考生来投考,国文考试卷上有一位考官出了个对子,上联是:孙行者,要求对下联。
大家没有一个对的好,只有一个学生勉强对了一个人是:胡适之。然而其实真正的答案是:祖冲之。
我们说到刘徽用割圆法得到了圆周率的值,那么什么是割圆法呢?我们先看看圆内接正六边形,如果圆的半径是1的话,那么六边形的每一边都是1,周长就是6。如果用圆内接正六边形近似圆周的话,就可以得到跟直径的比,也就是圆周率的近似值是3。如果像下面这张图,每一边都变成两条边,也就是说内接正多边形的边数翻一倍,根据刘徽得到的结论,边长就会更接近圆周。其实几何上可以证明,边长跟正多边形的面积是关联的,当正多边形边数越多,就越接近于圆,面积也就越接近于边长为一的圆面积,也就是圆周率的数值了。
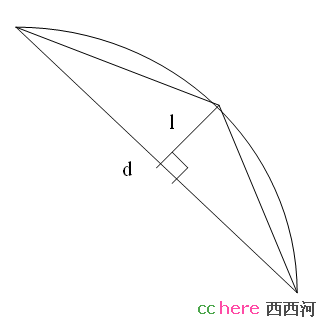
具体的操作,我们假设圆内接正n边形的边长是d,那么根据勾股定理,2n边形的边长就是sqrt(l^2+(d/2)^2)。怎么得到l的长度呢?这个也是初中几何的内容,根据勾股定理得到l=1-sqrt(1-(d/2)^2)。(才发现l和1不好区分,大家凑合看吧)所以最后得到的圆内接正2n边形的边长就是sqrt(2-2*sqrt(1-(d/2)^2))。现在看到了,每多倍增一次多边形的边数,要做一次平方,两次开方,还有其他的一些运算。用Excel可以很容易得到当时祖冲之运算的结果,我把边数,边长和总长度列出来如下:
6 1 3
12 0.51763809 3.105828541
24 0.261052384 3.132628613 0.026800072
48 0.130806258 3.139350203 0.00672159
96 0.065438166 3.141031951 0.001681748
192 0.032723463 3.141452472 0.000420521
384 0.016362279 3.141557608 0.000105136
768 0.008181208 3.141583892 2.62842E-05
1536 0.004090613 3.141590463 6.57109E-06
3072 0.002045307 3.141592106 1.64281E-06
6144 0.001022654 3.141592517 4.10545E-07
12288 0.000511327 3.141592619 1.02053E-07
24576 0.000255663 3.141592645 2.66804E-08
看,祖冲之算到24576边形,已经很接近圆周率了。
有人问,第四列是什么数?这个,呵呵,接下来,就是我自己的发挥了。我们注意到,每倍增一次边数,得到的圆周率越来越接近真值,那么每次增加了多少呢?这个就放在第四列了,表示比上一次运算增加的差值。仔细看看,发现一个有趣的规律:每次增加的差值基本上是以四分之一递减的。到了384边形,这个规律已经很明显了。我们现在要大胆假设,以后的增加也是以这个规律来的,那么后面我们就不再算了,而是改用四分之一递减的无穷级数的和来代替。从384以后,无穷级数的和是前一个差值0.000105136的三分之一,我们把这个值加到384边形边长3.141557608上面,就得到了3.1415926533。看!这个数跟圆周率在小数点后面第十位才有差别,比祖冲之的结果精确100倍。
当然,这是对割圆法的创新,用几乎百分之一的边数得到几乎一百倍的精确度。不过想一想祖冲之是在什么年代,拥有的是什么样的数学方法和计算工具。而我们学到现在掌握了多少现代的科学知识和工具,这点改进也就只能算游戏了。
本帖一共被 1 帖 引用 (帖内工具实现)
祖冲之,张衡……
看来是有的看了阿。![]()
古之九数,圆周率三,圆径率一,其术疏舛。自刘歆、张衡、刘徽、王蕃、皮延宗之徒,各设新率,未臻折衷。宋末,南徐州从事史祖冲之,更开密法,以圆径一亿为一丈,圆周盈数三丈一尺四寸一分五厘九毫二秒七忽,朒数三丈一尺四寸一分五厘九毫二秒六忽,正数在盈朒二限之间。密率,圆径一百一十三,圆周三百五十五。约率,圆径七,周二十二。又设开差冪,开差立,兼以正圆参之。指要精密,算氏之最者也。所著之书,名为《缀术》,学官莫能究其深奥,是故废而不理。
引自《隋书·律历志》
因为要斜穿北京市区,可以和女友一起多骑一阵车。
多谢,改过来了。
一种理论认为这是祖冲之采用“连分数”记数的自然结果。
简单说,祖冲之认为3.1415926<pi<3.1415927,取中值3.14159265用连分数表示为:
3 + 1 / ( 7 + 1 / ( 15 + 1 / ( 1 + 1 / 288 + 1 / (...) ) ) )
如果略去尾数,可得:
3 + 1/7 = 22/7,既疏率。
3 + 1/(7+1/15) = 333/106。
3 + 1/(7+1/(15+1/1)) = 355/113,既密率。
我个人认为这个理论解释很接近真实情况。
也是,超前了一千年吔。
如果是发表出来大概也能得个什么数学奖。
用这个方法在计算机上就可以算出无限多位小数,极限取决于计算机软硬件。
很希望读到一些真实的关于我们祖先的科学技术成就的介绍。