主题:【原创】中国古代的科学家们——数学家之祖冲之 -- 安德的游戏
- 共: 💬 38 🌺 66
我们说到刘徽用割圆法得到了圆周率的值,那么什么是割圆法呢?我们先看看圆内接正六边形,如果圆的半径是1的话,那么六边形的每一边都是1,周长就是6。如果用圆内接正六边形近似圆周的话,就可以得到跟直径的比,也就是圆周率的近似值是3。如果像下面这张图,每一边都变成两条边,也就是说内接正多边形的边数翻一倍,根据刘徽得到的结论,边长就会更接近圆周。其实几何上可以证明,边长跟正多边形的面积是关联的,当正多边形边数越多,就越接近于圆,面积也就越接近于边长为一的圆面积,也就是圆周率的数值了。
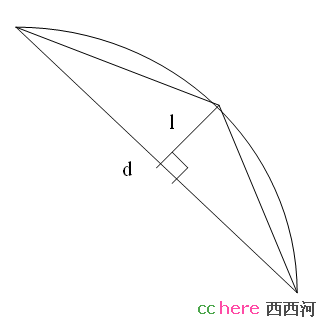
具体的操作,我们假设圆内接正n边形的边长是d,那么根据勾股定理,2n边形的边长就是sqrt(l^2+(d/2)^2)。怎么得到l的长度呢?这个也是初中几何的内容,根据勾股定理得到l=1-sqrt(1-(d/2)^2)。(才发现l和1不好区分,大家凑合看吧)所以最后得到的圆内接正2n边形的边长就是sqrt(2-2*sqrt(1-(d/2)^2))。现在看到了,每多倍增一次多边形的边数,要做一次平方,两次开方,还有其他的一些运算。用Excel可以很容易得到当时祖冲之运算的结果,我把边数,边长和总长度列出来如下:
6 1 3
12 0.51763809 3.105828541
24 0.261052384 3.132628613 0.026800072
48 0.130806258 3.139350203 0.00672159
96 0.065438166 3.141031951 0.001681748
192 0.032723463 3.141452472 0.000420521
384 0.016362279 3.141557608 0.000105136
768 0.008181208 3.141583892 2.62842E-05
1536 0.004090613 3.141590463 6.57109E-06
3072 0.002045307 3.141592106 1.64281E-06
6144 0.001022654 3.141592517 4.10545E-07
12288 0.000511327 3.141592619 1.02053E-07
24576 0.000255663 3.141592645 2.66804E-08
看,祖冲之算到24576边形,已经很接近圆周率了。
有人问,第四列是什么数?这个,呵呵,接下来,就是我自己的发挥了。我们注意到,每倍增一次边数,得到的圆周率越来越接近真值,那么每次增加了多少呢?这个就放在第四列了,表示比上一次运算增加的差值。仔细看看,发现一个有趣的规律:每次增加的差值基本上是以四分之一递减的。到了384边形,这个规律已经很明显了。我们现在要大胆假设,以后的增加也是以这个规律来的,那么后面我们就不再算了,而是改用四分之一递减的无穷级数的和来代替。从384以后,无穷级数的和是前一个差值0.000105136的三分之一,我们把这个值加到384边形边长3.141557608上面,就得到了3.1415926533。看!这个数跟圆周率在小数点后面第十位才有差别,比祖冲之的结果精确100倍。
当然,这是对割圆法的创新,用几乎百分之一的边数得到几乎一百倍的精确度。不过想一想祖冲之是在什么年代,拥有的是什么样的数学方法和计算工具。而我们学到现在掌握了多少现代的科学知识和工具,这点改进也就只能算游戏了。
本帖一共被 1 帖 引用 (帖内工具实现)
- 相关回复 上下关系8
🙂送花—— 履虎尾 字515 2007-05-15 19:46:41
🙂闹了半天,是因为没人看得懂 看看 字22 2007-05-16 00:29:53
😄看来这会成为一个系列了 水风 字44 2007-05-15 19:43:23
🙂【原创】补充一下割圆法

🙂从前面七个数据可以计算到误差约3*10^(-15) 1 大洋芋 字134 2007-05-17 05:49:18
🙂最后这个步骤 1 博德尔夫 字86 2007-05-16 11:13:12
🙂这个你“自己的发挥”是不是世界首创? njyd 字116 2007-05-16 00:59:21
🙂是不是世界首创我不知道 1 安德的游戏 字170 2007-05-16 15:41:41