主题:阿波罗尼奥斯问题-Prob. of Apollonius -- 理性网民
- 共: 💬 36 🌺 127
式(6.8)可以改写成为如下向量形式,并可以将其解表示成
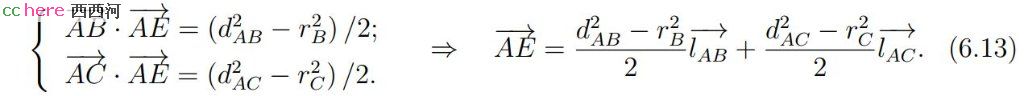
其中字母上的箭头表示连接两点的向量,而lAB、lAC分别表示与向量AC、向量AB垂直的向量,且满足如下关系

式(6.13)可以通过将等式两边同时与向量AB、向量AC做点积来验证。进一步可以验证
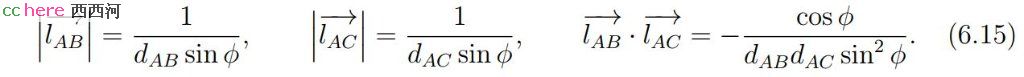
其中ϕ = BAC为向量AC、向量AB的夹角。
类似的,式(6.9)可以改写成为如下向量形式。其中,向量k沿x轴与y轴的分量即为kx、ky。
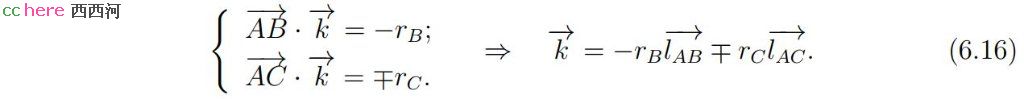
kx与ky的平方和即为向量k长度的平方。利用(6.15)式,可以得到
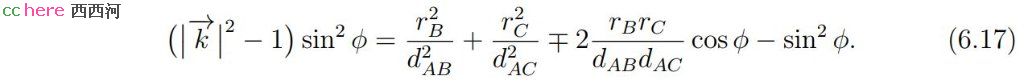
式(6.17)可以用来判断式(6.10)中二次项的系数。定义θB = rB/dAB、θC = rC/dAC,分别表示圆B、圆C相对于点A的半视角。当ϕ = θB ∓ θC时

ϕ = θB ∓ θC意味着当从点A观察圆B、圆C时,两圆圆心的视距离等于两圆的半视角之和或之差。也就是说,可以找到一条经过点A的直线与圆B、圆C相切。这意味着点A在圆B与圆C的公切线上。
为了证明式(6.11)与式(6.12)等价,注意到式(6.11)中方括号内的项即为向量AE与向量k的叉积的模。为了将叉积的模转化为点积,令与向量AE垂直的向量为
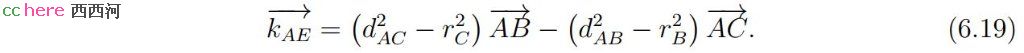
式(6.11)可以转化为
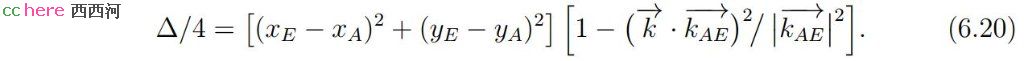
这样Δ与如下定义的Λ同号,且
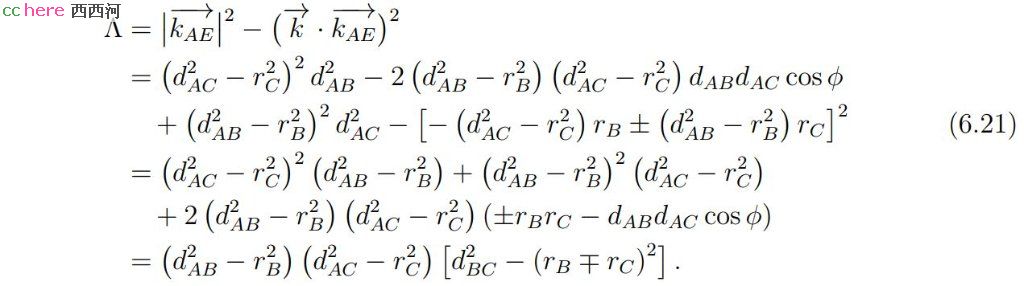
- 相关回复 上下关系8
🙂【7.1】解析几何方法 7 理性网民 字1092 2021-02-11 00:35:15
🙂【6】PCC问题 1 理性网民 字3141 2020-07-31 15:07:07
🙂【6.1】解析几何方法 理性网民 字2920 2021-02-07 13:13:58
🙂【补充】基于向量的公式推导

🙂【5】PPC问题 2 理性网民 字2007 2020-07-28 12:12:54
🙂【5.2】解的存在性和个数 1 理性网民 字960 2020-11-09 10:05:39
🙂【5.1】解析几何方法 1 理性网民 字2718 2020-10-16 12:06:53
🙂【补充】E点的几何意义 1 理性网民 字760 2020-10-16 12:09:49