主题:【原创】中国的效率与男人的智商 -- 同人于野
假设有200个不同的基金,最初的资金量相等。
在六十年里,每个基金的平均年收益都为 5%
现假设收益率的方差分别为 5%, 10% 和 20%
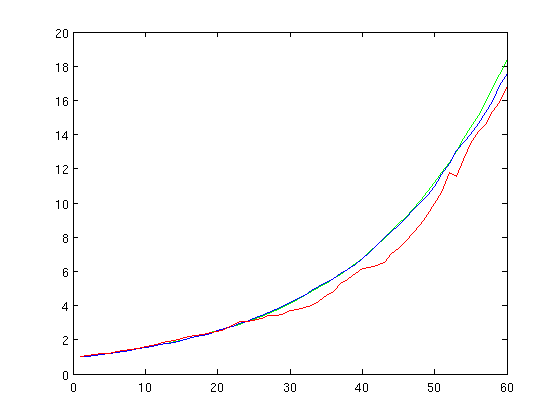
下面这张图是在以上三种不同的方差情况下,200个基金60年表现情况的均值
横轴为年份,纵轴为资金的扩展规模。
从这张图里我们可以看出,如果考虑的只是均值,三种方差并没有太大的区别。
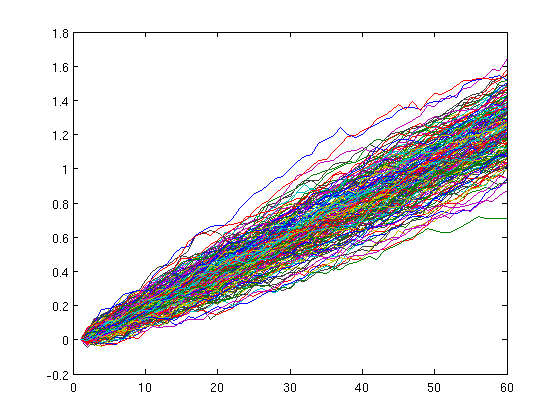
如果我们把每个基金的单独表现都画在一张图上
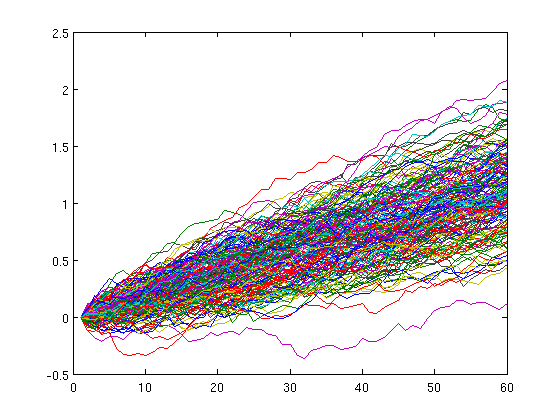
以下三张图的横轴依然为年份,纵轴为收益率的对数值(0代表没有变化,1代表十倍, -1代表缩水为初始值的十分之一)
方差 5%
方差 10%
方差 20%
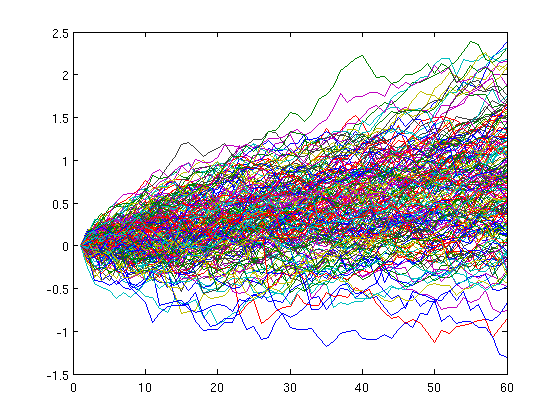
我们可以清楚的看到,在均值相同的情况下,数据的方差越大,最终各个基金表现的差异也越大。
当方差扩展到20%的情况下,对于某个单独的基金来说,风险已经无法控制。
最高的可能会有百倍的收益(10^2),但也有大量的缩水一半甚至更多。
用图说话,结果应该更直观一些了。
个人一直有一个假设,衡量一个国家的富裕程度,也许可以用这个国家历史上获得连续稳定税收的年份来做为一个指标。年份越长的,在复利的威力下,国家的富裕程度越高。
缺乏数据,所以一直没能验证。如果哪位网友有条件的话,倒是可以算算看。
附上所用的 matlab 程序,希望没有算错
n=200;
%x=[0:.01:0.2];
x=1;
for i=1:1:n
rpt1(i,:)=.05*randn(1,m) + 0.05;
rpt2(i,:)=.10*randn(1,m) + 0.05;
rpt3(i,:)=.20*randn(1,m) + 0.05;
end
evo1 = ones(n,m);
evo2 = ones(n,m);
evo3 = ones(n,m);
for i=1:1:n
for j=2:1:m
evo1(i,j) = evo1(i,j-1) .* (1+x*rpt1(i,j));
evo2(i,j) = evo2(i,j-1) .* (1+x*rpt2(i,j));
evo3(i,j) = evo3(i,j-1) .* (1+x*rpt3(i,j));
end
end
plot(mean(evo1),'g'); hold on;
plot(mean(evo2),'b'); hold on;
plot(mean(evo3),'r');
plot(log(evo1')/log(10));
plot(log(evo2')/log(10));
plot(log(evo3')/log(10));
- 相关回复 上下关系8
🙂其实博弈过程也和大多数西方人无关吧? 桥上 字0 2009-08-22 04:05:34
🙂纳粹政府是民选政府 7 夏侯梦得 字143 2009-08-21 05:08:44
🙂好文有宝 快刀浪子 字90 2009-08-20 17:11:00
🙂最近刚好在算一些有关复利的数据

🙂一天 笼中猪 字44 2009-08-20 13:01:28
🙂西方人没有弄明白或者故意不明白的是 2 Levelworm 字206 2009-08-20 12:53:00
🙂外国人未必不明白,他们也知道有博弈。从好的方面讲 一足无间 字88 2009-08-22 07:42:26
🙂制度各有利弊而以 光年 字295 2009-08-20 00:41:38