主题:【原创】上帝之书 -- 我爱莫扎特
- 共: 💬 277 🌺 1121
我对中国古代科学发展的了解不足,文中观点有失偏颇。据说李约瑟对中国古代数学家在勾股定理上的贡献有比较客观的论述,可惜我没看过他的书。
个人感觉,中国古代更多偏重于计算的技巧,有点今天“算法”学的意思,和古希腊那套互补性比较强。
去图书馆查了李约瑟的巨著,澄清了我的一些误解。
首先中国人是正儿八经的证明过勾股定理的,下图是三国时赵爽给《周髀算经》作的注。
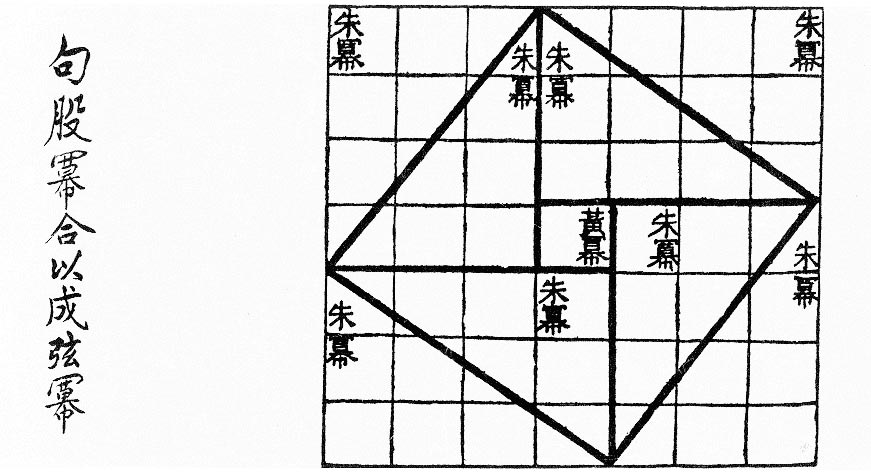
相当于证明了

不过时间上可能还是希腊人早一些。优先权之争需要确切的资料,年代太久很难讲清。
另外,古巴比伦人可能比希腊人还要早发现了勾股定理。
本来勾股定理打算写三块,写到第二块(中)的时候,又发现一次写不完,就出现了(中上)的标题。
结果资料越找越多,看来几何这部分至少要写成4,5段了,只好改标题。
每天象挤奶一样,真不知道晨枫,萨苏这些妖精是怎么修炼的。
这两天补了不少课,以前念书真是不认真啊!写到现在,大部分资料都来自wiki,Bell的《数学大师》,Klein的《古今数学思想》,同志们还是直接看这些书算了,我写得实在糟糕。唉。
还有回帖讨论好像不多,是我写得太浅了?还是太过无趣?
我不知道中国人没有证明勾股定理的讲法是哪里来的。 但这肯定是有问题的
也有说《周髀算经》是后世伪作的。但这不能作为实证。要讲历史,中国古代史官的负责态度至少是不会比西方人差的
即便是在欧洲。毕达哥拉斯定理的讲法也不是唯一的。我记得法国好像叫驴桥定理。还有印度也有自己的讲法。
勾股,毕达哥拉斯,驴桥,还有印度的定理出现时间几乎是相同的(考虑到当时的交流限制),讨论谁先谁后完全没有意义。
唯一的解释是古代各地劳动人民在生产实践中共同发现了这个定理![]()
积跬步,至千里,咱不要求跟那些老妖精一样,贴一篇就要酣畅淋漓,咱们有多少发多少,这个坑不少人蹲着呢,不信你看送花数阿,连你的冒泡贴都有人花。
嘿嘿,羽羊接着蹲坑去了,等下文阿~~~
转眼到了19世纪,几何学大变革的大幕即将拉开。
首先出场的是个匈牙利年轻人,名叫鲍耶(Janos Bolyai),和法国天才Galois很像,极具数学天分的他还具有勃勃的雄心。他的目标是通过反证法证明第五公设。为此,他提出相反的假设:过直线外一点有多于一条直线与原直线不相交。在前人大量工作的基础上,20岁不到的他发展出一套完整的理论,一套与欧式几何学非常不同的几何理论。和前人相同的是,他在这套理论中始终没有找到与其他公设的矛盾之处。不同的是,他向世人宣布,找不到矛盾是因为本来就没有矛盾!第五公设根本不可能被其他公设推导出来,因为它独立于其他公设。也就是说,他通过改变第五公设,发现了一种新的几何学。

几乎在同时,甚至更早些时候,俄罗斯有位名叫罗巴切夫斯基(Nikolai Ivanovich Lobachevsky)的数学家也做出了独立的工作。同前人们一样,他一直试图证明第五公设,有几次甚至以为自己已经成功,不久后又发现自己的错误。终于有一天他也醒悟了,他用同样的假设代替第五公设,得出了同样一套几何理论。他们同时独立发现的这套理论被后人称为Bolyai-Lobachevsky几何,又称为“双曲几何学”。

“双曲”和双沟大曲没关系。这是双曲函数的图像。亲切吧。:)
今天的我们也许很难想象这套“叛逆”的理论诞生时所经受的压力。罗巴切夫斯基的论文被圣彼得堡科学院置之不理,更长期被当地学术圈视为疯子,还常常收到匿名攻击。他的论文无处投稿,幸亏后来他当上了喀山大学的校长,利用一点职权在校刊上发表了论文。事实上他的工作大约到了几十年后才被世界承认。罗巴切夫斯基在俄罗斯孤独的一个人在战斗,直到去世前都没受到公开的支持。后人赞颂他为“数学中的哥白尼”。

而我们的小鲍耶显然也很清楚自己的处境,他明白以一人之力挑战整个学术圈的困难。聪明的人动起了小脑筋 ------ 找熟人开后门。鲍耶的父亲不仅研究工作出色,还认识不少学术名流。尤其是他和当时世界数学界的领袖------高斯是多年的同窗好友。
小鲍耶将工作寄给高斯,满心期待的他不久后收到了一封非常著名的回信:“我不能赞美你,因为赞美你就是赞美我自己。。。。。。你的工作,与我30多年前作出的发现几乎完全一样。。。。。。”任何人看到这样的回信恐怕都无法平静,更何况是年轻气盛而又刚刚做出惊人发现的小鲍耶。他与高斯彻底决裂,并严厉指责高斯是可耻的剽窃者。更可惜的是,鲍耶此后在学术方面再也没有做出新的贡献。
看过电影《莫扎特》(Amedeus)的朋友(没看过的朋友我强烈建议你们去看看)一定对影片中的大反派萨列里(Salieri)印象深刻,这位天才的宫廷音乐家无疑是最了解莫扎特艺术天分的人物,也正是这种了解让他无法忽视莫扎特对他地位的威胁,最后痛下杀手。如果把非欧几何的故事戏说成电影的话,说不定情节更离奇曲折,而大反派的角色,多半花落到高斯头上。
戏说归戏说,历史上的萨列里远非电影刻画的那么不堪。(据说萨列里家乡人民一直嚷嚷着要和电影剧组打官司)历史上的高斯到底和非欧几何有什么瓜葛呢?
本帖一共被 1 帖 引用 (帖内工具实现)
所以,说高斯是反派不恰当吧。
可是,这和勾股定理有虾米关系聂?等着。
挖坑的技术也不赖。。。。![]()
慢慢讲,慢慢讲。
勾股定理和我说的这些都有关系,但暂时回不过去。
老高的人品就和“伟大”不沾边了。呵呵。
假如认为列出一堆3,4,5;6,8,10;5,12,13等等就可以了,那么大家都一边玩去,人家巴比伦哥们比商高的著名谈话还早就刻了几十组在泥板子上了。
假如认为需要一个对一般情况的逻辑推理,那么貌似还是得叫希腊人一声“大葛阁”。人家没有画格子数数,而是对一般情况作出了论证。
特别的,赵爽这个只能算勾股定理的一个举例说明罢了,算不得正经证明。照这样画格子数,5,12,13就要数个半死,更不要说一般的非整数情况根本没办法这样画着证。
有些朋友可能会觉得这个“说明”和希腊“证明”本质上是一回事,因为可以很容易顺着这个说明里的图写出希腊证明来。但是要注意,这件事“容易”是因为现代人对实数已经有了充分的认识,有没有格子都一样;但是对于千年前的古人,从自然数到整数到有理数实数,每一步都是认识上的飞跃。你给赵爽个直角三角形两直角边1,根号e试试,八辈子他也未必证得出来。严格地说,毕达哥拉斯也证不出来,因为他不懂无理数。但是希腊几何证明的好处就在于,有理也好无理也罢,我总可以(严格地讲这是需要证明的,没有人对此苛求是因为这远远超出了整个人类的古代数学水平)做出几个正方形来切切分分,拼拼凑凑。更有甚者,拼凑中的面积比较依赖的不是数格子,而是欧式空间面积的平移不变性。这样就完全避开了有理无理的难题。
当然了,希腊人原版证明我也没看过,没准和赵爽这个一个档次。也可能赵爽知道如何证,但是象费马一样懒得写。不过鉴于希腊人是几何思维,中国人是代数思维,两个可能性都不大。
总之,以现代数学的观点看,希腊人比其他文明在层次上要高了一截。不过这和民族智力之类的东西无关,不过是希腊人吃饱饭没事干的人比较多,选择了门槛低的几何,其他民族与天地人斗忙得很,选择了门槛高的代数而已(注意并不是说这两个学科有高下之分)。纵观人类数学史,没有一个主攻代数的古代民族能够发展出超越中国古人高斯消去法的成果,更不用说原本类型的系统理论了。
很多论者觉得他有把现代思想塞入古人作品的倾向,和他不一样不算偏颇。
话说这边儿小毛孩子正和老学霸掐架,四周里里外外倒围了不少群众,可是看戏的多,丢花儿的少。花开二朵,各表一枝,咱们且由他们掐着,回头来看看这非欧几何究竟长什么模样。
其实早在一千多年前,人们就开始研究另一种几何学 ------ 球面几何学。球面上当然没有“直线”,取而代之的是“大圆” ------ 球面上以球心为圆心的的圆。“线段”则是大圆的圆弧。过球上任意不是对径点的两点,都有唯一的大圆把它们连起来。类似的,我们还可以定义两条大圆弧的夹角为相应切线的夹角。遗憾的是,由于任意两个大圆都有两个交点,球面几何并不在欧式几何的体系内(不符合前四个公理)。
球面几何是非常有用的几何,天上(天文),地上(地理)都用得着它。要是没有球面几何学,大航海时代恐怕很难到来,谁让地球是圆的呢?
.jpg)
人们没想到的是,只要稍作一点改动,球面几何就可以转化成另一种不同的非欧几何 ------ 椭圆几何。在这种几何中,过直线外一点的所有直线都与原来的直线相交。历史有时候真会和人开玩笑,我们千辛万苦寻找的东西,其实在很早就摆在我们身边,却不为人所知。这也许就是人们常说的“灯下黑”吧。
我们把球面几何和双曲几何放在一起看,有不少相似的“奇怪”性质。
球面几何里,(三条大圆弧构成的)三角形的内角和总大于180度。我们有

其中S是三角形面积,R是圆球半径,

而在双曲几何里,三角形的内角和总小于180度。我们有

其中S是三角形面积,c是某个正的常数,
从这些公式可以看出,三角形的面积越小,它越像欧氏几何。今天的我们知道,之所谓我们感觉自己生活在欧氏空间里,是因为我们生活的尺度和宇宙比起来太小太小了。(各位有没有想起狭义相对论?)
再比如说我们已经遗忘很久的勾股定理。前面提到过,勾股定理与第五公设是等价的。也就是说,勾股定理正是欧式几何的“基石”之一。非欧几何里不再成立勾股定理。但直角三角形的三边a,b,c(斜边)还是有些特殊的关系。
球面几何中:Cos(a/R)Cos(b/R) = Cos(c/R)
双曲几何中:Cosh(a)Cosh(b) = Cosh(c)
不过,这还不是勾股定理最后一次出现,后面的篇章中,我们会看到勾股定理更深刻的意义。
类似的古怪公式不少,我就不一一列举了。
科学史上每次出现新生事物总有个被误解然后慢慢被承认的过程。牛顿的无穷小量也好,虚数也好,都在很长的时间里被人们视为“幽灵”。罗巴切夫斯基发现了新的几何后,自己也觉得这个东西实在太古怪。他把这种几何称为“想象的几何”。要人们接受这种想象的几何实在不容易。罗巴切夫斯基试图将双曲几何和人们熟悉的球面几何联系起来,说服人们双曲几何只是球面几何的一个兄弟。他的想法是正确的,但他并未完全成功。
我们的主人公们虽然发现了好东西,可它实在古怪,令人难以相信。伟大的理论还需要优秀的推销员。爱因斯坦碰上了爱丁顿爵士(Sir Arthur Stanley Eddington),让广义相对论少受了几年委屈。若干年后,非欧几何终于迎来了一位好推销员 ------ 意大利数学家贝尔特拉米(Eugene Beltrami)。
本帖一共被 4 帖 引用 (帖内工具实现)
实际上麦克斯韦方程化简后只有四个,今天的麦克斯韦方程组就是这四个方程而已,没有八个。
能不能给说说?
我记得大学学习的好像是8个。物理盲,呵呵。