- 近期网站停站换新具体说明
- 按以上说明时间,延期一周至网站时间26-27左右。具体实施前两天会在此提前通知具体实施时间
主题:有趣的数学 -- 普鲁托
最近河里讨论概率的话题很热闹,俺也凑凑趣、跟跟风,写个主帖。
先出题:
学校有一个保送名额,有三位同学都合格,学校安排抽签决定谁保送。
方式:签筒里三个签,一个保送签,两个不保送签。三位同学按序抽签,每位同学抽完的签不再放回签筒。问:最后一位抽签的同学中签的概率比前两位如何?(答案在帖末)
=====================
现在说说孟同学那个三门问题的“悖论”:
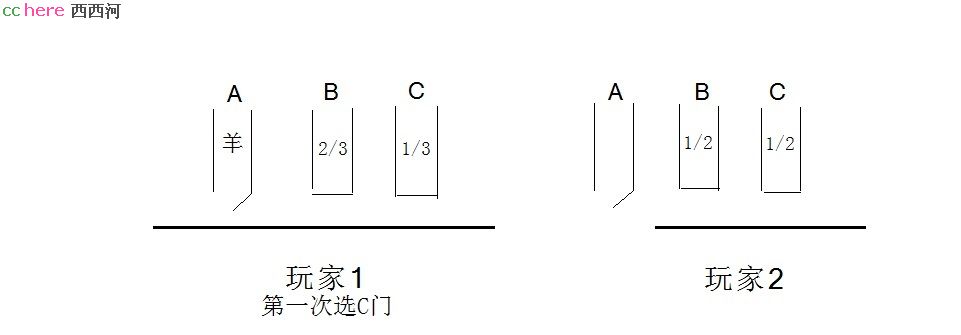
玩家2一上台什么都不知道,就知道BC两门里有一羊或车,他选中车的概率是1/2
玩家1第一次选C门,在主持人打开A门后,也只面对BC两门,也知道BC两门有一羊或车,为什么这时两门的有车概率就不是各1/2?
这不符合直觉。
================
首先,我们的直觉要接受一个观念,“有些行为会改变事件概率”。比如,当主持人打开A门后,对于玩家1来说A门里是羊2/3、是车1/3的概率就变成了:A门是羊的概率为1,是车的概率为0。同样,主持人打开A门后B、C门的概率也可能发生改变,这个情况不难理解。
“有些行为会改变事件概率”,这句话就是说有些条件变了,概率也会发生改变。这就产生了“条件概率”这个概念。
A表示事件,P(A)表示事件A发生的概率。P(A/B)表示在事件B发生的条件下事件A发生的概率,这就是条件概率。
一般人对条件概率会产生一个错觉,以为事件A在事件B发生的条件下的概率,与事件B在事件A发生的条件下的概率是一样的。
最有名的就是那个艾滋病检测的例子:艾滋病检测试剂准确率为99.9%,张三试剂检测阳性,那么张三得艾滋病的概率八九不离十。这是错误的,张三完全不必恐慌![]() 。
。
美国曾经有一个著名的案子,有律师用此来诡辩:在辛克利刺杀里根案中,辛克利的律师在法庭上指出:有相关医学资料显示,30%CT显示脑萎缩的人有精神病,而正常人只有2%。辛克利CT显示脑萎缩,所以辛克利很可能有精神病。当时控方律师没能接住,只是避开了这个诡辩。巧的是,辛克利最后确实被判有精神病。
事件A在事件B发生的条件下的概率,与事件B在事件A发生的条件下的概率是不一样【P(A/B)≠ P(B/A)】,但两者是有确定关系的,贝叶斯公式就是这个关系的数学陈述:P(B/A)= P(A/B)* P(B)/P(A)。
下面是我对三门问题的解答,只需要用到贝叶斯公式和全概率公式,不感兴趣的河友请略过:
。
2、设事件a、b、c分别表示三个门被打开,P(a)、P(b)、P(c)分别表示打开三个门的概率。打开某个门的概率是多少,暂不表。
现在,玩家1选中了C门,主持人打开了A门,此时求:B门、C门是车的概率各是多少?
利用贝叶斯公式,在A门被打开的条件下,B门里是车的概率为:
P(B/a)= P(a/B)* P(B)/P(a)
这里面,P(a/B)是什么?是玩家1选C门而B门是车时,主持人打开A门的概率。玩家选了C,而B门又是车,所以主持人只能打开A门,即P(a/B)= 1
有点麻烦的是P(a),即打开A门的概率是多少?
根据全概率公式:P(a)= P(a/A)P(A)+ P(a/B)P(B)+ P(a/C)P(C)。【它直观意义就是一个事件的概率可以把它看成是各个“小条件”下各概率的和,这些“小条件”刚好合起来成为事件完整的大条件】。
P(a/A)是玩家1选C门而A门是车时,主持人打开A门的概率。显然主持人不可能打开A门,因为里面是车。所以,P(a/A)= 0
P(a/C)是玩家1选C门而C门是车时,主持人打开A门的概率。显然主持人此时既可能打开A门,也可能打开B门,所以 P(a/C)= 1/2
那么
A门被打开的概率P(a)= P(a/A)P(A)+ P(a/B)P(B)+ P(a/C)P(C)= 0*(1/3)+1*(1/3)+(1/2)*(1/3) =1/2
现在,最终结果,B门是车的概率P(B/a)= P(a/B)* P(B)/P(a)= 1*(1/3)/(1/2)=2/3
同样,在A门被打开的条件下,C门里是车的概率为P(C/a)= P(a/C)* P(C)/P(a)= (1/2)*(1/3)/(1/2)= 1/3
需要注意的是,在主持人的一翻骚操作中,他是上帝视角。
最后说说那个保送抽签的问题,三位同学不论抽签先后顺序,中签的概率都是1/3。同学们都不用争先恐后地抢着去抽,完全不用担心前面的同学把保送名额抢先抽走了。
生活中有很多抽签的事件,买房、买车都要限购、抽签,排先排后抽,都没有关系。股票打新也是,9点半下单和下午两点下单,中签概率是一样的。
让人保持淡定,数学不但有趣,还能有这点好处![]() 。
。
- 相关回复 上下关系8
🙂有趣的数学

🙂有趣的是还真有一堆专家研究 1 光头佬 字84 2021-05-17 05:46:59
🙂这个理论上还是有可能的 假设 字397 2021-05-18 03:56:20
😄与常识相反的东东就是讨厌 1 燕人 字12 2021-05-16 16:12:23
🙂常识是个奇怪东西 2 普鲁托 字100 2021-05-17 00:46:15
🙂这个要看前面的结果公布还是不公布 8 假设 字922 2021-05-16 05:34:08
🙂以公布的方式抽签,会怎样? 1 普鲁托 字606 2021-05-17 05:30:52
🙂那如果有两个保送名额呢? 假设 字6 2021-05-18 03:50:14