主题：阿波罗尼奥斯问题-Prob. of Apollonius -- 理性网民

问题：给定两条直线l、m和以A为圆心的圆，找出与l、m以及圆A相切的圆（如图）。

解：将直线l、m平移一定距离分别得到直线n、p。该距离与圆A半径相等。过圆心A与直线n、p相切做圆（PLL问题），圆心为O点，与n、p分别相切于B、C两点。过O点做圆与圆A相切，则其同时与l、m相切，故为所求。

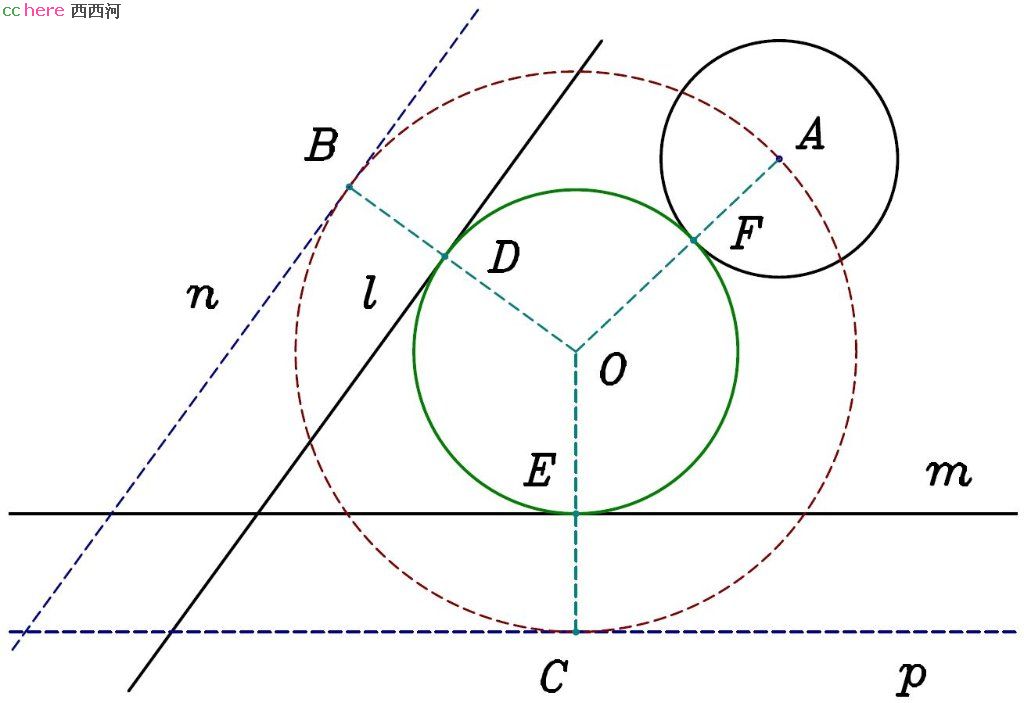
证明：连接O、A两点，那么所求圆与圆A的切点F在线段OA上。同样连接O、B两点及O、C两点，所求圆与l的切点D在线段OB上，所求圆与m的切点E在线段OC上。OB与l、n都垂直，故|DB|等于l、n之间的距离，|DB| = |FA|。同理，OC与m、p都垂直，故|EC| = |FA|。因为A、B、C三点在以O点为圆心的圆上，|OA| = |OB| = |OC|，又|DB| = |EC| = |FA|，所以|OD| = |OE| = |OF|，即D、E、F三点在以O点为圆心的圆上。

分析：在平移l、m时，平移的方向应当同时远离圆A，或者同时靠近圆A。首先考虑l、m相交的情况。当平移的方向为远离时，总会得到两个解，并且得到的圆与圆A外切。当平移的方向为靠近时，依赖于圆A与l、m的相对位置，有两个解或者没有解，并且得到的圆与圆A内切：当圆A与l、m不相交时，或者圆A与l、m都相交时，有两个解；当圆A与l、m中的一条相交时，无解。所以在l、m相交时，LLC问题有四解或两解。类似地可以考虑l、m平行的情况。注意到当圆A位于l、m外侧时，问题无解。

评论：PPP问题、PPL问题、PLL问题和LLC问题组成了阿波罗尼奥斯问题的第一个系列。一般来说，一个系列中排序靠后的问题可以转化为其所在系列中排序靠前的问题。后面可以看到，除了LLL问题以外，所有的阿波罗尼奥斯问题最终都可以转化为PPP问题进行求解（LLL问题也有转化为PPP问题的解法）。

在PPP系列中，我们可以看到两个特别的技巧。其中一个出现在PPL问题中，即反演中心O的存在。这将是后面的PPC问题、PCC问题及PLC问题的求解关键。另一个出现在LLC问题中，即通过直线的平移（及圆的半径的变化），将问题中的某个定圆转化为定点。这将在后面的CCC问题及LCC问题中出现。