- 近期网站停站换新具体说明
- 按以上说明时间,延期一周至网站时间26-27左右。具体实施前两天会在此提前通知具体实施时间
主题:【原创】纳什均衡即为势--对博弈论的分析 -- baiqi
你举的这个例子,诠释当中有不少需要补充的内容,正好博弈论是我的论文方向,而我导师也有一篇很有意思的文章研究过石头剪刀布游戏。
首先,“如果没有混合策略模型”是个超级大的假设。这三个策略是如此的对称,因此最有意义的均衡自然是每个玩家以1/3,1/3,1/3的混合策略参与游戏。你提出的其实是一个已有不少理论研究话题,即有多个Nash Equilibria时的Equilibrium Selection问题。因为某些原因settle在某个特定的均衡上(如两人出包)是可以的,但是需要一些额外的东西来break the symmetry,比如你提到的熟人之间的默契,类似于focal point的解释。
接下来说那个自然的混合策略,我导师提出的问题是,真的就必然要收敛到这个混合均衡吗?回答这个问题需要之前game theory没有太多深究的一样东西,即off equilibrium dynamics:玩家在尚未到达均衡之际(其实大部分时间都是off equilibrium的)是如何对别人的策略做出反应的。简单说一下结论,如果是个good Rock-paper-scissors game(比如赢了得1,输了扣0.5),那么混合策略是收敛且稳定的;而要是个bad Rock-paper-scissors(赢了得1,输了扣2),那才有趣,不收敛,且只要稍有扰动就会奔一个围绕着1/3,1/3,1/3打转转。
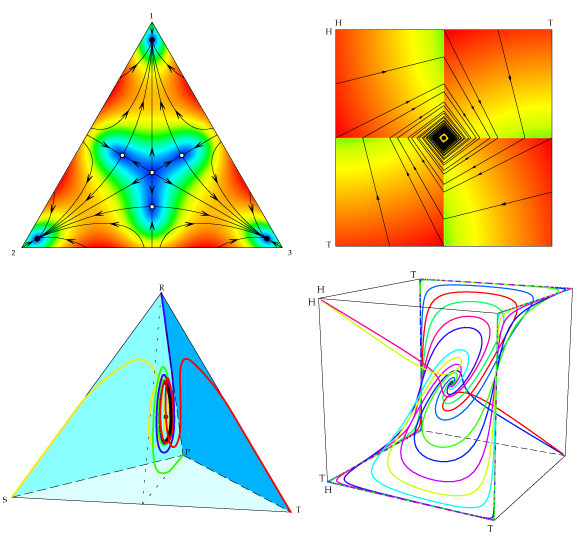
注:上图仅左下角的那个金字塔描述了RPS game,其他三张无关本主题,请忽视。
而且如果是带平局的Rock-paper-scissors,混沌可以观察到。
- 相关回复 上下关系8
🙂【原创】纳什均衡即为势--对博弈论的分析 43 baiqi 字3786 2010-06-05 02:01:06
🙂谢钱 wwwfarm 字152 2010-09-29 08:41:37
🙂补充一下

🙂重复博弈相比一次博弈产生了质变 4 baiqi 字1500 2010-07-21 23:44:23
🙂我认为重复博弈的和一次博弈的本质不同是 5 海神八尖叉 字754 2010-08-14 08:27:00
🙂这就是一个数学问题 酥油茶 字68 2010-06-06 01:54:46