主题:【原创】勾股定理(九)--- 坐标 -- 我爱莫扎特
- 共: 💬 19 🌺 42
坐标的发明,是数学史上值得大书特书的历史性事件。这个简单而不平凡的工具,彻彻底底的改变了几何学的风貌。
坐标,是一座桥梁,将“形”和“数”完美的结合了起来。有了它的帮助,我们可以把纯粹的几何问题转化为代数的计算。许多曾令人耗尽脑汁的几何难题突然迎刃而解。欧式几何这门人类最古老的数学分支之一,在坐标诞生之后,即被人类彻底征服。
不仅如此,在计算机发明之后,人类更是开始探索“机器自动证明”方法。20世纪七十年代后期,中国数学家吴文俊通过研究代数方程的性质,在平面几何的机器证明上取得一系列重要突破。用他的方法,不仅能证明已有的几何定理,还能发现新定理。此后,欧式几何不仅对人们不再困难,连机器都可以轻松搞定。

坐标的思想如此简单,让人很难理解人类为何花了那么久的时间才掌握它。其实,坐标思想的雏形,大概早在千年之前就有,但当时的人们对代数计算的掌握远远谈不上充分。直到距今350年前,法国大数学家,大哲学家笛卡尔(Rene Descartes)终于能熟练掌握今天高中生所熟知的那套数学工具,从而将人们一直朦朦胧胧略有了解的坐标思想清晰的表达了出来,一举奠定解析几何的基础,也为后来的微积分提供了成长的土壤。
而且,笛卡尔坐标系的思想在代数学领域也得到了很大的发展,为了研究高维欧式几何,必须发展对应的代数工具,这就是今天理工科大学生必修的“线性代数”。
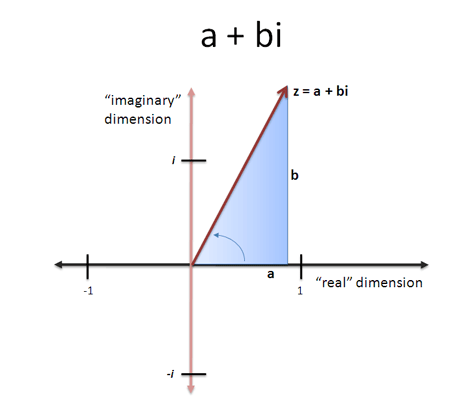
这种“形”与“数”互相转化的思想简明易懂,人们似乎早已习惯而感受不到它的伟大之处。但伟人的心灵似乎是相通的。与前辈笛卡尔一样,高斯非常清楚坐标的力量。笛卡尔用坐标将“形”转化为“数”,而高斯则用坐标将“数”转化为“形”。在人们对复数(即实数加上虚数)还心存疑虑的时候,高斯第一个提出可以将复数看作平面上的点。这样一来,对复数的研究很容易转化为对几何的研究。这个简单的思想,直接改变了此后近200年整个数学的面貌。
此后,高斯的思想被他的学生黎曼进一步深化。为了研究复变函数(即以复数为自变量的函数,这类函数与实变函数差异很大),黎曼经常考虑函数的几何性质。作为一个典型的例子,可以参看我爱莫扎特:【原创】看得见的数学之Mobius变换

由于复变函数的特殊性质,黎曼还特地发明了一种几何对象 --- 黎曼面(Riemann Surface)。这或许是20世纪数学家最喜爱的几何对象了吧。它的影响甚至超出科学之外。不少艺术家以此为题作画,比如Escher的名作《画廊》(Print Gallery)就是画在黎曼面上的。
[MP=480,480]http://escherdroste.math.leidenuniv.nl/clips/bclip_1_1.mpg[/MP]
更有甚者,Aldous Huxley在小说《美丽新世界》(Brave New World)中,有种流行的体育运动叫“黎曼面网球”,想必是非常困难的运动。
======
好久没更新,实在是自己的事情很忙。坐标这篇本来打算写到微分几何的局部坐标系,不过写得太长了,就先贴一半上来,剩下的已经接近完成,很快贴上来。
另外,感谢河友支持我成为认证会员。也请大家积极回复,告诉我你们的意见。
本帖一共被 2 帖 引用 (帖内工具实现)
- 相关回复 上下关系8
🙂【原创】勾股定理(九)--- 坐标

🙂很多图都看不了啊 侠之大者 字0 2009-07-13 11:04:34
🙂Escher的画超级酷 胡丹青 字175 2009-05-21 16:11:43
🙂嗯,我老人家早年下过一个论断 马大善人 字64 2009-05-21 22:26:40
🙂能不能展开讲讲? 我爱莫扎特 字54 2009-05-22 02:38:33
🙂咄,知道是微言还要刨根问底? 1 马大善人 字1183 2009-05-22 13:51:22