- 近期网站停站换新具体说明
- 按以上说明时间,延期一周至网站时间26-27左右。具体实施前两天会在此提前通知具体实施时间
主题:【翻译】概率随机及编程 (一) -- 东方射日
生日错觉
这里有一个很好的例子有助于大家理解我们上述讨论的概率。这就是经典的生日错觉问题。这就是说,如果有23个人在一间屋子里,那么其中至少有两个人生日相同的概率将大于50%。这和我们的直觉好像是矛盾的,但是数学上却可以证明这是真的,我们的直觉是错的。“BirthdayOdds”问题要求你计算最少需要多少人才能使两个人的生日相同的概率大于某一值。
首先,我们可以注意到互补的问题可能更容易解答:“N个随机的人生日各不相同的概率是多少”。解决的思路就是从一个空房间开始,逐一添加一个个人,计算生日与里面所有已有人不同的概率。
int minPeople (int minOdds, int days)
{
int nr;
double target, p;
target = 1 - (double) minOdds / 100;
nr = 1;
p = 1;
while (p > target)
{
p = p * ( (double) 1 - (double) nr / days);
nr ++;
}
return nr;
}
这个所谓的生日错觉有很多实际的应用,其中之一就是“Collision”问题。算法和上面基本是一样的,有一个要注意的事项是,有时事件本身可能会改变样本空间。
有时,一些概率问题是比较费解的,例如上面所的生日错觉问题似乎违背了我们的常识。但是利用前面的公式,我们可以计算出正确的结果。不过你如果想成为一个概率专家,还需要更多的对数字的“感觉”。这种感觉一部分是天生的,另一部分可以后天通过学习和练习来培养。做一下外链出处上的测试,你一则可以了解自己对数字的感觉,二则也会对一些基本的概率问题有更多的理解。
概率计算
在本章中,我们将采用一些例题来计算非独立事件的概率,也就是说一件事件的发生将影响随后事件发生的概率。我们可以用图来组织这些事件,节点是时间,边是事件间的依赖关系。在我们计算不同事件的概率时,很类似于我们在图上前进。我们从图的根节点开始,这就是事件开始前的初始状态,并且可以设置根节点的概率为1。然后依据不同的情况,我们考察概率是如何响应分布的。
嵌套的随机数
Nested Randomness 问题。(大致就是计算随机函数嵌套情况下的概率,具体描述请上topcoder参看)
这一问题看起来让人退缩。但是据说有人已经指出,这只是几条线的问题。
第一步,我们很明确我们要做什么,随机函数Random(N)被调用并返回一个在0到N-1间均匀分布的随机整数。这样,也就是说每个整数出现的概率是1/N。如果我们将这一结果作为下一次调用随机函数的输入,我们可以得到所有Random(Random(N))结果的概率。为了好理解,我们以N=4为例:
第一步,各个整数有相同的概率1/4
第二步,以下四个函数各有1/4的可能被调用Random(0);Random(1);Random(2);Random(3).Random(0)返回错误,Random(1)返回0;Random(2)各有1/2的可能返回0或1;Random(3)则各有1/3返回0,1或2
第三步,Random(0)有1/4+1/8+1/12的可能性被调用,Random(1)的可能性则为1/8+1/12;Random(2)的可能性为1/12
类似的,第四步,Random(0)的可能性是1/4而Random(1)的可能性是1/24
第五步,我们只有Random(0)的可能
所有过程在下图中描述:
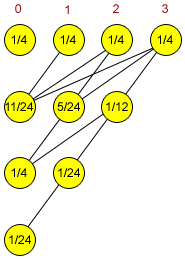
源代码如下:
double probability (int N, int nestings, int target)
{
int I, J, K;
double A[1001], B[2001];
// A[I] represents the probability of number I to appear
for (I = 0; I < N ; I++) A[I] = (double) 1 / N;
for (K = 2; K ≤ nestings; K++)
{
for (I = 0; I < N; I++) B[I] = 0;
// for each I between 0 and N-1 we call the function "random(I)"
// as described in the problem statement
for (I = 0; I < N; I++)
for (J = 0; J < I; J++)
B[J] += (double) A[I] / I;
for (I = 0; I < N; I++) A[I] = B[I];
}
return A[target];
}
如果你在这个问题上有点心得,你可以再试试以下五个问题:
ChessKnight问题:为每个棋盘格分配一个该路,每一次移动计算下一步每格的概率
DiceThrows问题:计算两个玩家扔骰子各种可能的结果
RockShipping 问题:采用同样的思路,确定你定义了正确的湖的模型
PointSystem问题:用可能的(x,y)矩阵来建立时间的采样空间
VolleyBall问题:类似于上一问题
本帖一共被 1 帖 引用 (帖内工具实现)
- 相关回复 上下关系8
🙂好贴子 平面几何 字119 2008-12-18 22:40:13
🙂【翻译】概率随机及编程 (二)

🙂【翻译】概率随机及编程 (三) 8 东方射日 字5721 2008-12-18 22:12:21
🙂啊,算法研究要支持~ 1 弦子 字426 2008-12-18 22:41:45
🙂神经网络算法和随机算法 2 东方射日 字1137 2008-12-18 23:35:07
🙂沙发. 沉宝 字0 2008-12-18 21:53:32