主题：不是有关梦中情人的八卦 -- 荷子

===

看来无论科普还是八卦，都是个技术活啊，俺还需要学习提高。

感谢社长，感谢阿姨，感谢送花和没送花的朋友。

闲话少说，先把这个足球八卦完成了吧。

首先列出我们上次已经知道的常识

1.足球是对称的多面体

2.足球有60个顶点

3.足球由正五边形和正六边形组成

4.五边形有五个顶点五条边，六边形有六个顶点六条边

5.任何多面体，每条边由两个面公用

6.只要没有三角形，任何多面体的每个顶点处都是三个面

好了，开始数数。

假设一共有F5个五边形和F6个六边形

那么一共有 F=F5+F6个面，根据常识4，一共有 E=5F5+6F6 条边，V=5F5+6F6个顶点...

抱歉抱歉，要是这么算就完蛋了，再说我们的常识5和6还没用上呢。

每条边被用了2次，那么一共有 E=(5F5+6F6)/2 条边

每个顶点被用了3次，那么一共有 V=(5F5+6F6)/3 个顶点

然后呢？

嗯，实在不好意思，不得不引进一个公式了。这个公式是如此的大名鼎鼎，从这里可以引出一系列伟大的名字——高斯，欧拉，庞加莱，陈省身...和拓扑学，整体微分几何等等一系列数学分支...

打住打住，不说无聊的了，给公式吧

V-E+F=2

就是说，对于任何正多面体，顶点数（1维）-边数（2维）+面数（3维）=2

对于平面上的多边形自然也成立，只需要把它看成多面体的投影，最外面的轮廓算作一个面就行

这叫做多面体欧拉公式，这种交错和（奇数项为正而偶数项为负）的形式可以推广到高维，右面那个2是拓扑性质，称为欧拉示性数，一个更伟大的定理——高斯-博内定理把局部的曲率和这一全局拓扑性质联系起来，陈省身最大的成果就是给出了高斯-博内定理的内蕴证明。

说句题外话，关于这个公式的历史，有一本书叫做《证明与反驳》，读过之后可以知道，不仅仅是男人，女人，兄弟，组织不可靠，连逻辑，也不可靠。

怎么样？可以说颠覆性不亚于哥德尔不完备定理和海森堡测不准原理吧。开个玩笑，其实是更严谨，更深刻地认识了什么是证明。

好，有了这个公式，我们的足球数数问题就可以解决了，下面的计算完全是加减乘除。

V=(5F5+6F6)/3

E=(5F5+6F6)/2

F=F5+F6

因为V=60

那么5F5+6F6=180

那么E=(5F5+6F6)/2=90

V-E+F=2

那么F=32

F5+F6=32

5F5+6F6=180

那么F5=12，F6=20

结论，足球是一个12个正五边形和20个正六边形组成的多面体。

怎么样，是不是还是觉得很无聊很不八卦？

其实，阿姨说得对，我们还有个更好的方法——直接数数就知道了，而且，迄今为止，我们的常识1似乎还没有用到啊？别急

-------------------------下面是完全数数的方法-------------------------

好，让我们来看看足球，每个五边形的边上的五个图形是什么？每个六边形的边上又是什么？

五边形有5个对称轴，而5是个素数，所以——每个五边形的边上必须是5个一样的图形，才能保证对称，但我们可以知道，这5个一样的，不能是五边形，因为这样一来，只要整个足球上有一个五边形，所有的都是五边形了。

六边形有6个对称轴，可以有两种对称形式——全是一样的图形，或者两两相间的序列（您要是打过六个人的扑克游戏比如够级就很容易理解）也就是说可能每个六边形的边上全是五边形，或者3个五边形和3个六边形。

然而，因为每个顶点处有三个面，那么在五边形的一个顶点处的两个六边形，必然是相邻的，所以每个六边形的边上是3个五边形和3个六边形。

好了，我们再来看看这样两句话

每个五边形的边上是5个六边形

每个六边形的边上是3个五边形和3个六边形

您有什么结论？

五边形和六边形的比例是3:5

有了这个条件，我们就完全可以不用公式了

只要知道了

V=(5F5+6F6)/3=60和

F5:F6=3:5

同样可以得到

F5=12，F6=20

这就是伟大的对称

-------------------------完全数数的方法结束-------------------------

其实，还有更进一步的结论

回到C60

假如我们知道一个多面体只有正五边形和正六边形组成，那么有什么结论呢？

V=(5F5+6F6)/3

E=(5F5+6F6)/2

F=F5+F6

V-E+F=2

那么(5F5+6F6)/3-(5F5+6F6)/2+(F5+F6)=2

非常奇妙的，我们得到了F5=12

就是说，如果一个多面体只有正五边形和正六边形组成，无论有多少个正六边形，正五边形有且只有12个

当然，正六边形最少是0个，这时候就是正十二面体——每个面都是正五边形。

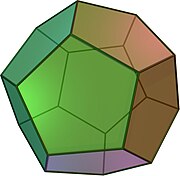
注意，下面的标示错了，是正十二面体。

好了，这个八卦就到这里吧，

最后还有几个小尾巴，究竟是现有的足球，还是先有的C60？

除了C60，还有C70等等，它们的结构有何特点？

为什么说足球其实是正十二面体或者正二十面体切出来的？而且，还是最简单最接近球的“半正多面体”？

正二十面体

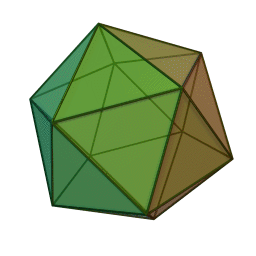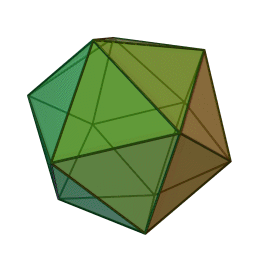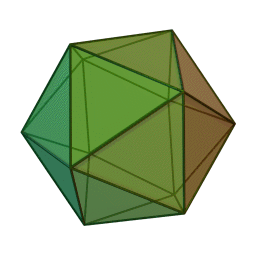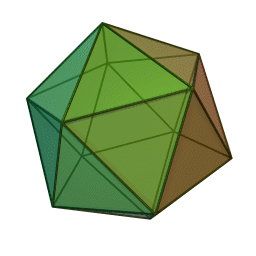
通过对正二十面体截角生成的C60

从一个五边形出发画足球

为什么说正十二面体和正二十面体相互对偶？

为什么说只有5种正多面体（每个面都是相同的正多边形），柏拉图毕达格拉斯开普勒是如何把它和宇宙万物特别是行星轨道联系起来的？

找行星轨道图的时候

不小心发现原来有一篇这个了安德的游戏:【原创】闲谈科学之正多面体（续四）

哈哈，幸好咱没去科经版，还是在这儿有社长阿姨地主喜欢罩着好

看到qiaozi:【原创】今天的数学（系列）里面不爱吱声:数学太抽象了,的帖子，非常赞同，事实上，从某种角度上说，物理学就是几何学的实现。

我们的直觉也许很难超越函数和方程，但对于几何，无论是被许多数学家所崇拜的“对数学一窍不通”的埃舍尔的画（他画出了所有的17种二维平面分割（镶嵌）模式）还是简单的足球，这里面蕴含的美是我们每个人都能够体会的，而格式塔学派等心理学所注意到的错觉以及画家们所熟知的的射影原理，其中蕴含的的美学和哲学等深刻的哲理，也是我们每个人都会思考的。

埃舍尔的画

另一方面，对于数字和图形的迷信和崇拜却又从古至今从来没有停止过，倘若我们多知道一些，就会少被骗一些。马丁加德纳的一本《矩阵博士的魔法数》是戳穿这种数学占星术的很好的例子。

先到这里吧，八卦得不好，抱歉了。

===

• 老兄一片保卫西西河的热心，不必客气啦