主题：【原创】庖丁解字 之 烟涛微茫： 中国古代数学的无穷思想 上 -- 丁坎

上文说道，微以手抉微，眇以目视小。微取象于飘散的发丝，而眇取象于散落的点(小为三点，少为四点，义同。) 微眇表现的不是不同的小，而是成为人类认识对象的小。

由此，微与眇均发展成为中国哲学的重要概念。

微眇共举已在道德经第一章中得到表现。

而由于语言发展的不平衡性，微字似乎得到了更多关注，在历史舞台上占有了更重要的地位，

例如在下面的哲学思考中：

道德经说：

用今天的语言来说，实际上就是刻划道不为人类视觉，听觉和触觉所企及，超越了感觉的极限。注意，搏与微的组合，也是对我们推断的一个验证。

庄子.秋水

今传道德经河上公注，在搏之不得名曰微之后注解到：

以上还仅仅是在哲学思考，但是，我们可以注意到，微已经开始表示

搏之不得的无形的小，这种小，与数学上的无穷小的之间的联系已经呼之欲出，只等一个数学家张口呐喊。

魏晋时期的刘徽就是这样一个应运而生的数学家。

在介绍刘徽的工作之前，我们需要交代一点预备知识：

中国古代数学具有强烈的应用性，在几何学上的体现是，数学家们的考虑对象是在社会生活中常见的特殊几何形体，而没有进行一般化处理。

这些形形色色的特殊形体的名称正如沈括说：

下图所示是一些常用的形体，其中前三个是我们今天主要处理的对象：

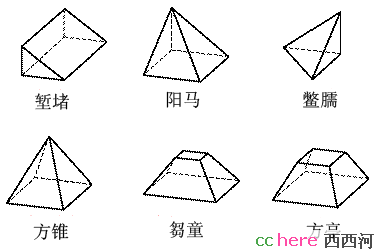
堑堵（沿长方体对角面切割而得的楔形立体）

阳马（直角四棱锥）

鳖臑（四面均为直角三角形的四面体）

设堑堵的长宽高分别为a,b,c，易见堑堵体积为abc/2,因为两个这样的堑堵可以拼成一个

长宽高分别为a,b,c的长方体，而长方体的体积为abc。

那么长宽高分别为a,b,c的阳马体积是多少呢？

大约成书于西汉末到东汉初之间的《九章算术》里有这个问题的解答：

即说阳马体积等于abc/3。

《九章算术》里给出了算法，但没有给出对算法的解释，让人对这个算法无法完全信从。

刘徽为《九章算术》作注时开始着手给出阳马体积求法的合理解释。

用论坛语言来说，就是《九章算术》的作者挖了个坑，刘徽试图帮他填坑。

坑有小有大，这个坑呢？

很大！大到一个平庸之辈把一生填进去也填补不满。因为当时处理这类体积问题的方法主要是通过对已经体积求法的

几何形体进行切割，期望将切割后的几何体重新组合，可以得到待求体积的几何形体，从而求得其体积。而这个方法

对付这个坑是无能为力的。

1900年，德国数学家希尔伯特在巴黎的国际数学家大会上提出了23个数学问题(23个大坑！)，为二十世纪的数学发展指定方向。

其中第三个问题是这样的：

若有任意两个体积相等的多面体，能否通过有限次切割，将第一个多面体组装为第二个多面体？

这个问题由希尔伯特的学生 Max Dehn 解决了，答案是否定的。

也就是说多面体体积问题必须引入无穷思想才能得到解答。

刘徽填坑的时候大约是在十几个世纪之前的公元三世纪中叶，他面临的困难可想而知。

我们今天已经不知道这个坑里填入了他多少苦苦思索的日夜，多少反复拼砌的几何模型，多少呕出的心血，但是我们知道，他把这个大坑填平了，而且，用的关键概念是微。

他的论证过程是：

其数学含义大略如下：

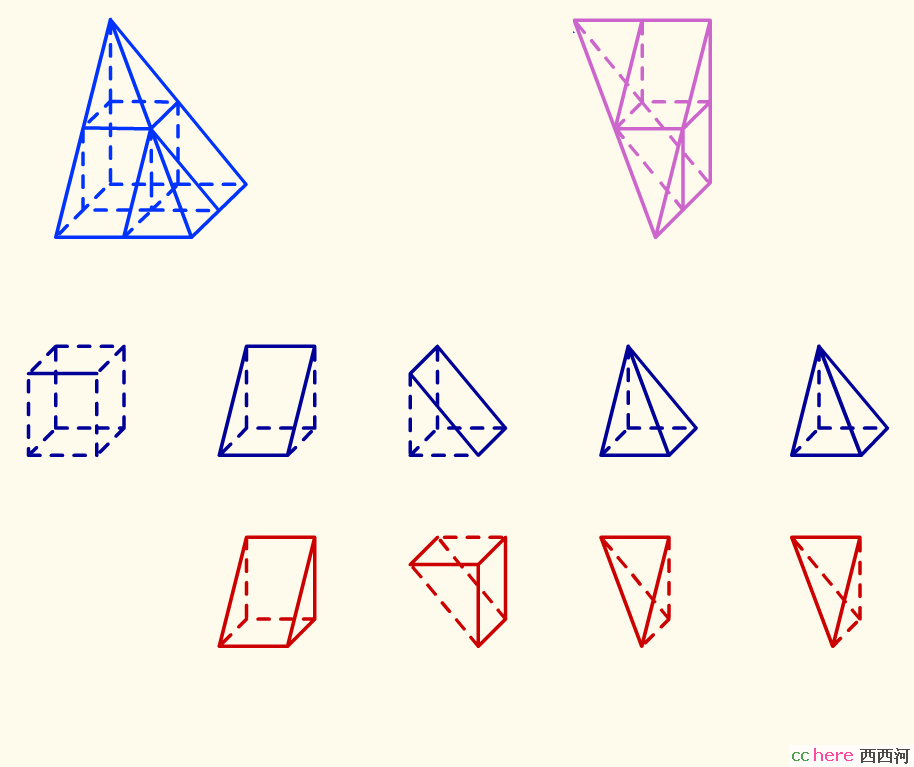
如上构造的鳖臑包含四个部件：两个小堑堵和两个小鳖臑，均为红色。

阳马包含五个部件：一个小立方，两个小堑堵和两个小阳马，均为黑色。

显然，来自鳖臑的两个小堑堵体积为来自阳马的一个小立方，两个小堑堵体积之和的1/2。

鳖臑剩余的两个小鳖臑与阳马剩余的两个小阳马体积之比呢？

按照上面的方法继续操作，鳖臑与阳马的体积比，已知部份始终是1/2，而未定部份取决于不断变小的小小鳖臑与小小阳马之比。

由于这样操作每次尺度减半，鳖臑与阳马的尺度如同一个无穷的等比数列：

1，1/2，1/4.........

用现代的语言来说，这个数列是收敛的且极限为0。

用刘徽的话来说：半之弥少，其余弥细。至细曰微，微则无形。由是言之，安取余哉。

(刘徽文中说到的1/4是就体积而言，我们说1/2是就线度而言，只求叙述方便，没有区别。)

于是，我们可以确定，鳖臑与阳马的体积比是1/2，在它们组成的堑堵中，阳马的体积是2/3，

所以，阳马的体积=堑堵*2/3=abc/2* 2/3= abc/3 .

刘徽对阳马体积的求索，不禁又让我们想起 烟涛微茫信难求 的诗句。

瀛洲虽微茫，犹有舟楫可渡。而无穷小之烟涛微茫，让普通人只能望洋兴叹：欲济无舟揖。

刘徽天才思想造就的舟楫是古代探险无穷世界的冲锋舟，更是今世我辈仰而有愧的丰碑。

参考文献：

郭书春 中国古代的无穷小分割思想 外链出处

Donald B. Wagner An early Chinese derivation of the volume of a pyramid:

Liu Hui, third century A.D.

外链出处

清华大学“中国科技史数字图书馆资料库”

外链出处

附记：应该还有个补，不过今天太累了，看看大家有什么问题再说。