主题：【原创】素数狂想2000年 -- lucase

本文原为山东大学数学院刘建亚院长为数学系基地班的新生所作的演讲。现整理并补充相关的资料后集结成篇。

素数狂想2000年

2，3，5，7，11，13，17，19，23，29，31，37，41，43，47，53，59，61，67，71，73，79，83，89，97，101，103，107，109，113 这些数是什么数？对，他们有一个共同的名字——素数

伟大的德国数学家高斯(Johann Carl Friedrich Gauss 1777年4月30日－1855年2月23日)外链出处曾经说过，“数学是科学的女王，数论则是数学的王冠。”

18世纪最伟大的数学家约瑟夫·路易斯·拉格朗日，(Joseph-Louis Lagrange，1736年1月25日－1813年4月10日)在数论和数学的其他分支以及物理学和天体力学方面都做出过重要的贡献。当他在研究出“每个数都是四个整数平方和”这个定理之后说，“对我来说，算数（数论）是最难的。”

法兰西科学院院士Jacobian说过，“上帝是算数学家。”

“数统治宇宙”

数统治宇宙这样狂的话，出自古希腊最著名的数学家——毕达哥拉斯外链出处。毕达哥拉斯在雅典创建了毕达哥拉斯学派。他对自然数、分数、有理数等各个领域都做出过杰出的贡献。他还曾经用整数的比例问题来研究音乐中的和弦问题。

罗素曾经这样评价过毕达哥拉斯，“我不知道还有什么别人对于思想界有过像他那么大的影响，我所以这么说，是因为所谓柏拉图主义的东西倘若加以分析，就可以发现在本质上不过是毕达哥拉斯主义罢了。有一个只能显示于理智而不能显示于感官的永恒世界；全部的这一观念都是从毕达哥拉斯那里来的。如果不是他，基督徒便不会认为基督就是道；如果不是他，神学家就不会追求上帝存在与不朽的逻辑证明”。但是当毕达哥拉斯发现 圆周率、开方2 等无理数时，大为震惊。他的学生 Hipparsus of Tarentum 向外人透露 无理数 的存在，其后便给毕达哥拉斯淹死了。不知道这算不算最早的学术迫害。

讲过以上这些以后，我们不得不认识到，有一类数在数学的研究中有着基本的重要性，那就是素数。在此我们不可避免的要提到素数的定义：素数，又称质数，一个大于1的自然数中，除了1和此整数自身外，没法被其他自然数整除的数；即是只有两个正因数（1和自己）的自然数。如果我们有兴趣查看一下素数序列的话，就会发现其中唯一的偶数2，而其他的素数则都是奇数。素数是构成全体整数的基本元素，任何一个正整数都能写成素数方幂的乘积。比如2385就可以分解成3的平方，5的平方和11的平方的乘积。

那么在知道了上述的情况之后，我们会问，素数在整个整数序列中是如何分布的呢？如何判断一个整数数否是素数呢？

早期的数学家们的实验结果让人很沮丧，基本上属于数手指头的方法。我们只能通过检验一个数是否可以被前面的整数整除。但是当这个数非常大的时候，使用这个方法的结果大概只有崩溃一条路可走了。

如果我们查看前人留下的素数表的话会发现，素数的分布是没有规律可以遵循的。素数的分布是一个随即的过程。所以曾经有人试图找到一个能够源源不断的产生新的素数的通项公式。当然结果是失败的。但是令人欣慰的是，我们可以找到一个很简单的证明这个想法是错误的方法。

如果从整个数轴的角度考察素数的分布，我们无异于大海捞针。那么我们可以取一个(0,x)的区间，考察这个区间内素数的分布情况。当然，这个X也是趋于无穷大的。但是尽管X趋于无穷大，却怎么也追赶不上数轴的箭头，所以X总也跑不到头。那么，我们记(0,x)这个区间上素数的个数为π(x),在此用π来标记素数的个数是因为π这个希腊字母对应的拉丁字母是P，而P正好是素数这个单词的第一个首字母。那么，我们可以得到这样的结论，随着x的逐渐增大，π(x)也是随之发生变化的。

我们又不可避免的要提到另外一个伟大的古希腊数学家欧几里德(约前330年—前275年)外链出处他的《几何原本》被誉为影响人类历史的三部著作之一。另外的两部，其中之一肯定是bible了，还有一本，不清楚。欧几里德对素数理论的贡献是，他证明了整数集中包含了无穷多个素数。

欧几里德

说完了素数的一些基本概念，我们要开始看素数定理了。

先看一下素数定理的定义外链出处：对正实数x，定义π(x)为不大于x的素数个数。数学家找到了一些函数来估计π(x)的增长。以下是第一个这样的估计。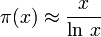

其中ln x为x的自然对数。上式的意思是当x趋近∞，π(x) 和x/ln x的比趋近1。但这不表示它们的数值随着x增大而接近。

如果我们注意这个公式的一个推导，π(x)/x = (x/lnx)/x = 1/lnx →0 暨素数的密度为0.那么我们可以看出，在整数序列中随机选择一个整数，它是素数的概率趋向于0，因此素数是特别稀疏的。

这个最早的推测是由德国数学家高斯和法国数学家勒让德(Adrien-Marie Legendre，1752年9月18日–1833年1月10日)完成的。

让我们再多说几句高斯。在知道高斯这个名字之前，我不相信数学界真的有天生奇才这种说法。直到有一天，我知道了高斯。高斯在12岁的时候（12岁的时候我们在干吗？）就知道要用同余式来统一整个的算数。15岁的时候就推测出了素数定理，但是很遗憾，他无法给出证明。

伟大的高斯

法国数论家勒让德

高斯是世界上为数不多的几个被印在钱上的数学家。

前联邦德国10马克

接下来我们会继续讲切比雪夫等同志是如何围绕数论展开研究的……